Chapter 7: Inertia
7.4 Mass Moment of Inertia
7.4.1 Intro to Mass Moment of Inertia
Mass moment of inertia, or inertia as it will be referred to from here on, is resistance to rotation. The bigger the inertia, the slower the rotation. [latex]\sum M = I\alpha[/latex]. Inertia is always positive and has units of kgm2 or slugft2.
For an infinitesimal unit of mass, the inertia depends on how far it is from the axis of rotation.
$$ I = \int_m r^2dm $$
As shown in this image, each little dm at a distance r from the axis of rotation (y) is added up (through integration). If r is bigger, the inertia is bigger.
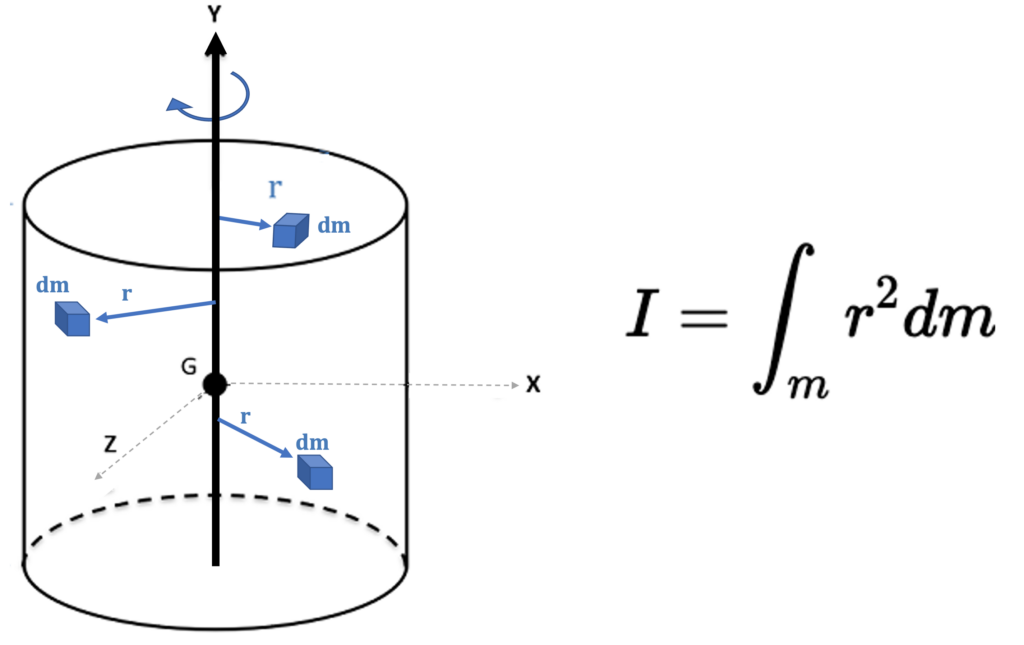
If there is more mass closer to the axis of rotation, the inertia is smaller. A skill that you can develop is your visualization of the rotation about each axis. As shown in the following figure, rotating about the different axes will produce different types of rotation. You can imagine sticking your pencil into an object and twisting along that axis. In this image, rotation about the y-axis and x-axis produces different types of rotation. Due to the symmetry, rotation about the x-axis and z-axis looks identical.
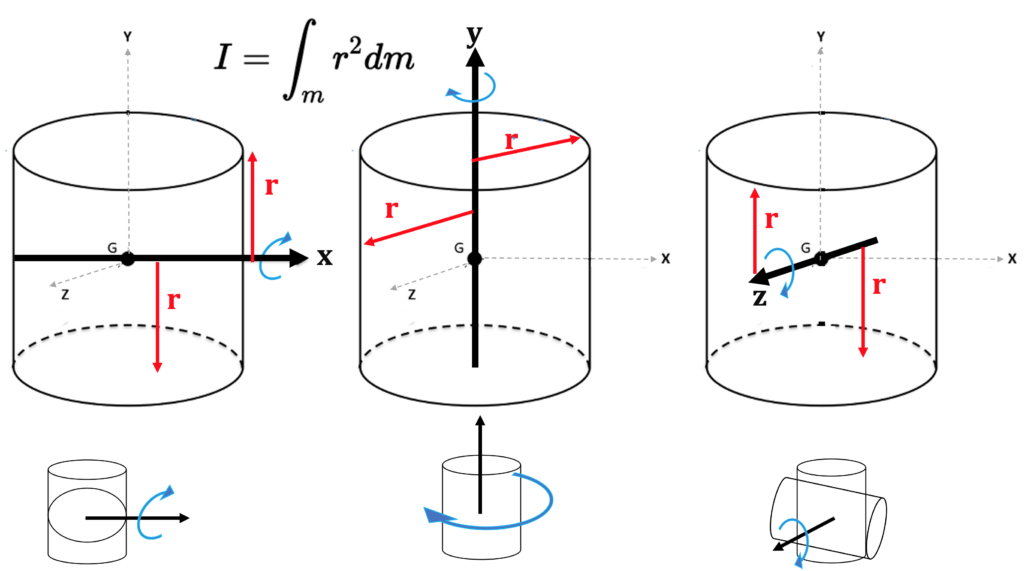
The red r’s in this image show the distance that is being measured when adding up each little infinitesimal dm. Notice how the r changes direction from x to y, but looks the same between x and z.
Equations have been developed for common shapes so that you don’t have to integrate every time you want to find the inertia of an object. The result is different for each axis, as shown in the following figure.
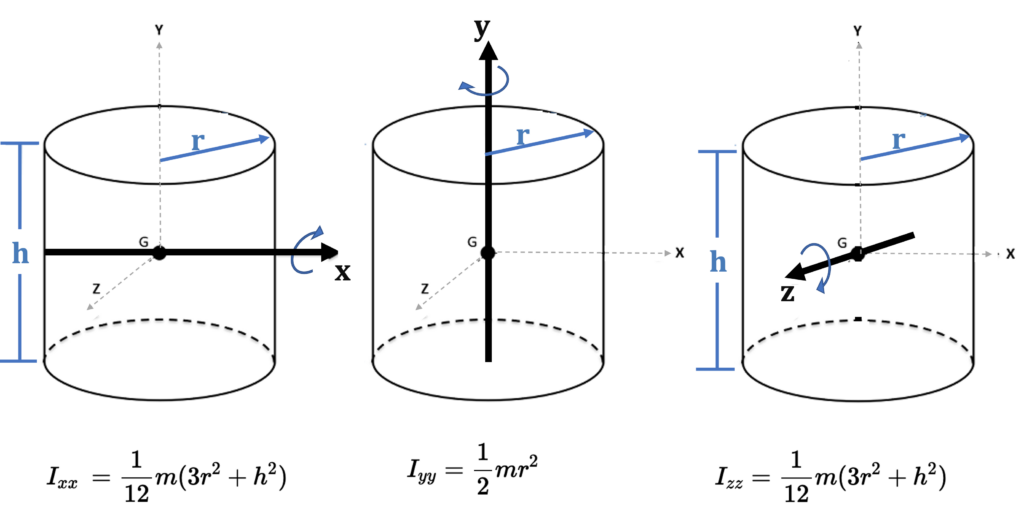
‘Ixx‘ can be read as ‘the inertia if rotating about the x-axis’. Notice for Ixx and Izz that the height and radius of the cylinder affect the inertia, whereas for Iyy, only the radius is considered.
The equations for each of the objects are listed in a table below. The first is a second explanation of inertia.
We start by constructing, in our minds, an idealized object for which the mass is all concentrated at a single location, which is not on the axis of rotation: Imagine a massless disk rotating about an axis through the center of the disk and perpendicular to its faces.
Let there be a particle of mass m embedded in the disk at a distance r from the axis of rotation. Here’s what it looks like from a viewpoint on the axis of rotation, some distance away from the disk:
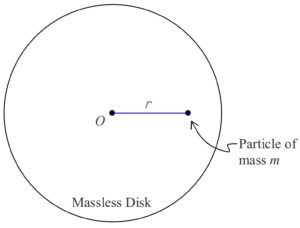
where the axis of rotation is marked with an O. Because the disk is massless, we call the moment of inertia of the construction the moment of inertia of a particle with respect to rotation about an axis from which the particle is a distance r.
I = mr2
The equation above is our equation for the moment of inertia of a particle of mass m, with respect to an axis of rotation from which the particle is a distance r.
Now, suppose we have two particles embedded in our massless disk, one of mass m1 at a distance r1 from the axis of rotation and another of mass m2 at a distance r2 from the axis of rotation.
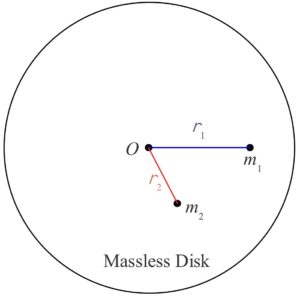
The moment of inertia of the first one by itself would be
I1 = m1r12
and the moment of inertia of the second particle by itself would be
I2 = m2r22
The total moment of inertia of the two particles embedded in the massless disk is simply the sum of the two individual moments of inertia.
I = I1 + I2
I = m1r12 + m2r22
This concept can be extended to include any number of particles. For each additional particle, one simply includes another miri2 term in the sum where mi is the mass of the additional particle and ri is the distance that the additional particle is from the axis of rotation. In the case of a rigid object, we subdivide the object into an infinite set of infinitesimal mass elements dm. Each mass element contributes an amount of moment of inertia
dI = r2dm
to the moment of inertia of the object, where r is the distance that the particular mass element is from the axis of rotation.
Source: Calculus-Based Physics 1, Jeffery W. Schnick. https://openlibrary.ecampusontario.ca/catalogue/item/?id=ce74a181-ccde-491c-848d-05489ed182e7
7.4.2 Inertia Table of Common Shapes
Specific inertia equations depending on the shape of the object and axis of rotation can be found below. Notice some of the shapes have multiple sets of axes: [latex]I_{xx} \text{ and } I_{xx}^\prime[/latex]. There are multiple equations.
| Symmetric Shapes | ||
| Thin Ring | 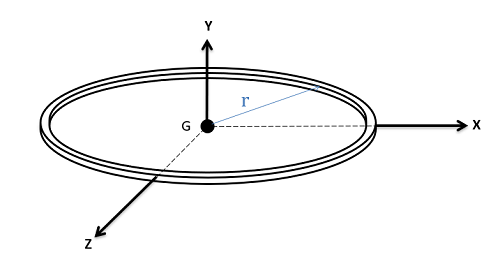 |
$$ I_{xx} = \frac{1}{2}mr^2 \\I_{yy}=mr^2 \\I_{zz} = \frac{1}{2}mr^2 $$
* thickness << 1 |
| Circular Plate | 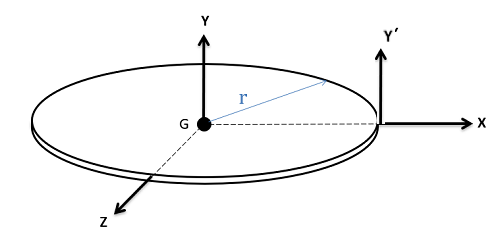 |
$$ I_{xx} = \frac{1}{4}mr^2 \\I_{yy}=\frac{1}{2}mr^2 \\I_{zz} = \frac{1}{4}mr^2 $$
$$ I_{yy^\prime} = \frac{3}{2}mr^2 $$
* thickness << 1 |
| Cylinder | 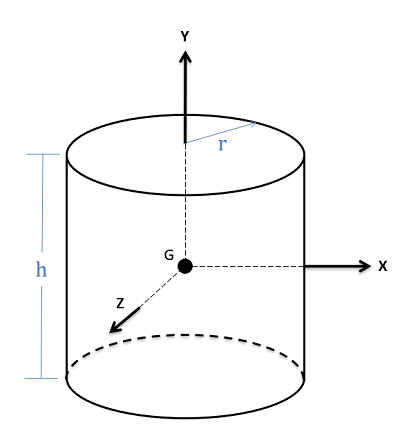 |
$$ I_{xx} = \frac{1}{12}m(3r^2+h^2) \\I_{yy}=\frac{1}{2}mr^2 \\I_{zz} = \frac{1}{12}m(3r^2+h^2) $$
$$Volume = \pi r^2 h $$ |
| Sphere | 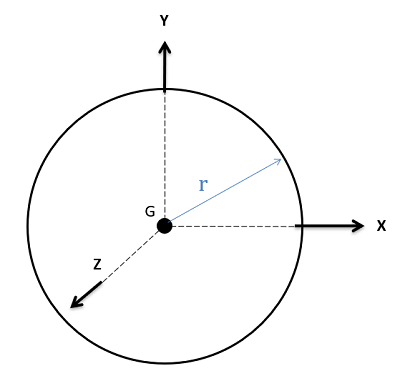 |
$$I_{xx}=\frac{2}{5}mr^2 \\I_{yy}=\frac{2}{5}mr^2 \\I_{zz}=\frac{2}{5}mr^2 $$
$$Volume = \frac{4}{3}\pi r^3 $$ |
| Slender Rod | 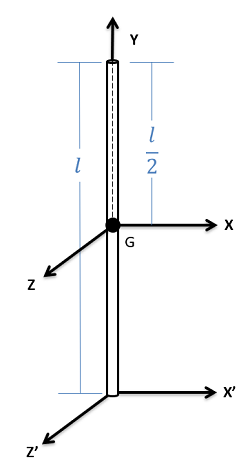 |
$$ I_{xx} = \frac{1}{12}ml^2 \\I_{yy}=0\\I_{zz} = \frac{1}{12}ml^2 $$
$$ I_{xx^\prime} = \frac{1}{3}ml^2 \\I_{zz^\prime} = \frac{1}{3}ml^2 $$ * radius << length |
| Rectangular Plate | 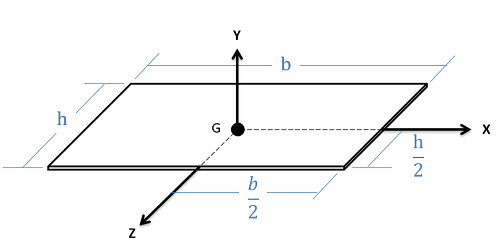 |
$$ I_{xx} = \frac{1}{12}mh^2 \\I_{yy}=\frac{1}{12}m(h^2+b^2) \\I_{zz} = \frac{1}{12}mb^2 $$
* thickness << 1 |
| Rectangular Block | 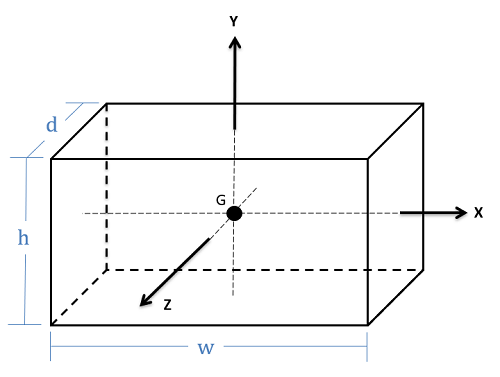 |
$$ I_{xx} = \frac{1}{12}m(h^2+d^2) \\I_{yy}=\frac{1}{12}m(d^2+w^2) \\I_{zz} = \frac{1}{12}m(h^2+w^2) $$
$$ Volume = bwh $$ |
| Asymmetric Shapes | ||
| Half Cylinder | 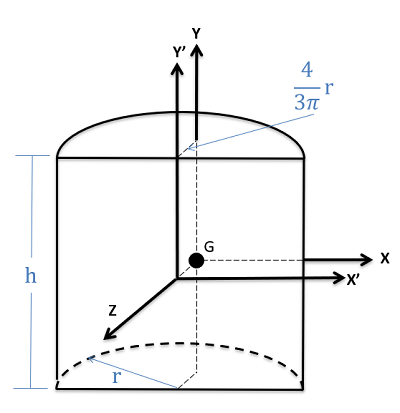 |
$$ I_{xx} = \left( \frac{1}{4}-\frac{16}{9 \pi^2} \right)mr^2 + \frac{1}{12}mh^2 \\I_{yy}= \left( \frac{1}{2}-\frac{16}{9 \pi^2} \right) mr^2 \\I_{zz} =\left( \frac{1}{4}-\frac{16}{9 \pi^2} \right)mr^2 + \frac{1}{12}mh^2 $$
$$ I_{xx^\prime} = \frac{1}{12}m(3r^2+h^2) \\I_{yy^\prime} = \frac{1}{2}mr^2)\\I_{zz^\prime} = \frac{1}{12}m(3r^2+h^2) $$
$$Volume = \frac{1}{2} \pi r^2 h $$ |
| Hemisphere | 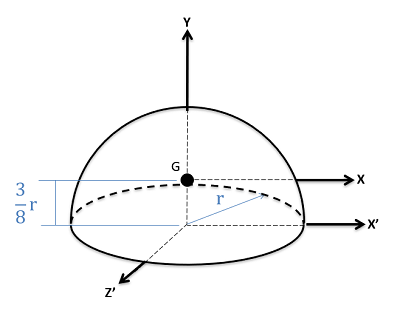 |
$$I_{xx}=\frac{83}{320}mr^2 \\I_{yy}=\frac{2}{5}mr^2 \\I_{zz}=\frac{83}{320}mr^2 $$
$$I_{xx^\prime}=\frac{2}{5}mr^2 \\I_{zz^\prime}=\frac{2}{5}mr^2 $$
$$Volume = \frac{2}{3}\pi r^3 $$ |
| Cone | 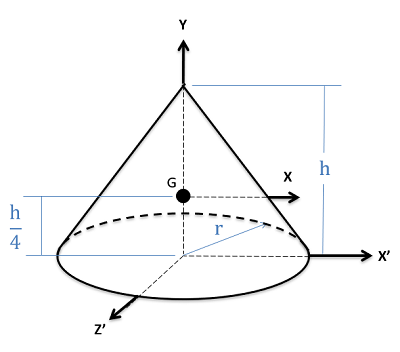 |
$$I_{xx}=\frac{3}{80}m(4r^2+h^2) \\I_{yy}=\frac{3}{10}mr^2 \\I_{zz}=\frac{3}{80}m(4r^2+h^2) $$
$$I_{xx^\prime}=\frac{1}{20}m(3r^2+2h^2) \\I_{zz^\prime}=\frac{1}{20}m(3r^2+2h^2) $$
$$Volume = \frac{1}{3}\pi r^2h $$ |
| Hallow Shells | ||
| Cylindrical Shell | 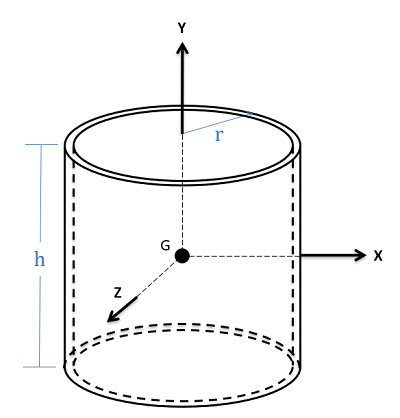 |
$$ I_{xx} = \frac{1}{6}m(3r^2+h^2) \\I_{yy}=mr^2 \\I_{zz} = \frac{1}{6}m(3r^2+h^2) $$
* Thickness << 1 |
| Spherical Shell | 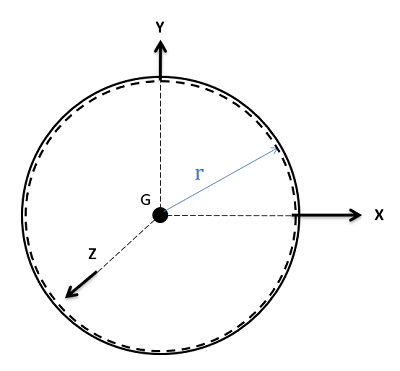 |
$$I_{xx}=\frac{2}{3}mr^2 \\I_{yy}=\frac{2}{3}mr^2 \\I_{zz}=\frac{2}{3}mr^2 $$
* Thickness << 1 |
| Hemispherical Shell | 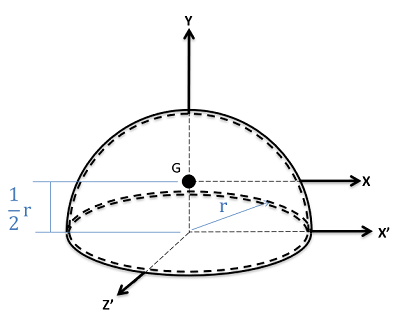 |
$$I_{xx}=\frac{5}{12}mr^2 \\I_{yy}=\frac{2}{3}mr^2 \\I_{zz}=\frac{5}{12}mr^2 $$
$$I_{xx^\prime}=\frac{2}{3}mr^2 \\I_{zz^\prime}=\frac{2}{3}mr^2 $$
* Thickness << 1 |
| Images source: Jacob Moore et al. http://mechanicsmap.psu.edu/websites/centroidtables/centroids3D/centroids3D.html | ||
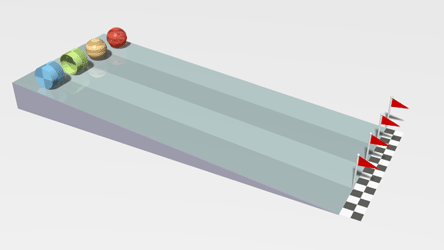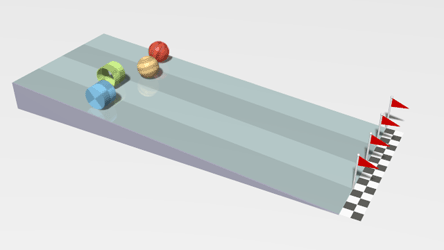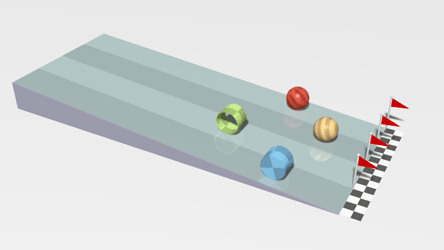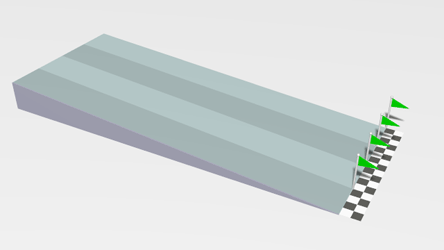
Notice how different objects with the same mass and radius rotate at different rates. This simulation shows a cylinder (blue), a ring (green), a solid sphere (yellow-brown), and a spherical shell (red). Which one has the least inertia? Why?
7.4.3 Radius of Gyration
A concept called the radius of gyration (k) converts a shape into a thin ring. This is used for particularly complex shapes. If a homework problem says ‘the radius of gyration k = 15 cm’, that means if the shape were a thin ring, it would have a radius of 15 cm. You calculate the mass moment of inertia using the ring equation: [latex]I = mk^2[/latex]
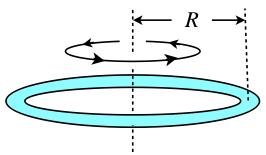
[latex]\qquad I = mk^2[/latex]
For example, if the mass of an object is m=10 kg, the radius of gyration is 5 m, then the inertia is:
I = mk2 = 10 kg * 5 m * 5 m = 250 kgm2.
To find the radius of gyration:
$$ k=\sqrt{\frac{I}{m}}=\sqrt{\frac{250 kgm^2}{10kg}} = 5 m $$
Key Takeaways
Basically: Mass moment of inertia is an object’s resistance to rotation and is impacted by mass and distance from the axis of rotation.
Application: The speed at which something rotates, such as a satellite spinning in space, is impacted by its inertia. A bigger inertia has a smaller angular acceleration. A smaller inertia allows for a larger angular acceleration.
Looking Ahead: This will be used throughout dynamics. The next section looks at calculating the inertia of composite objects or from a different axis.

