Chapter 1: Fundamental Concepts
1.5 Cross Products
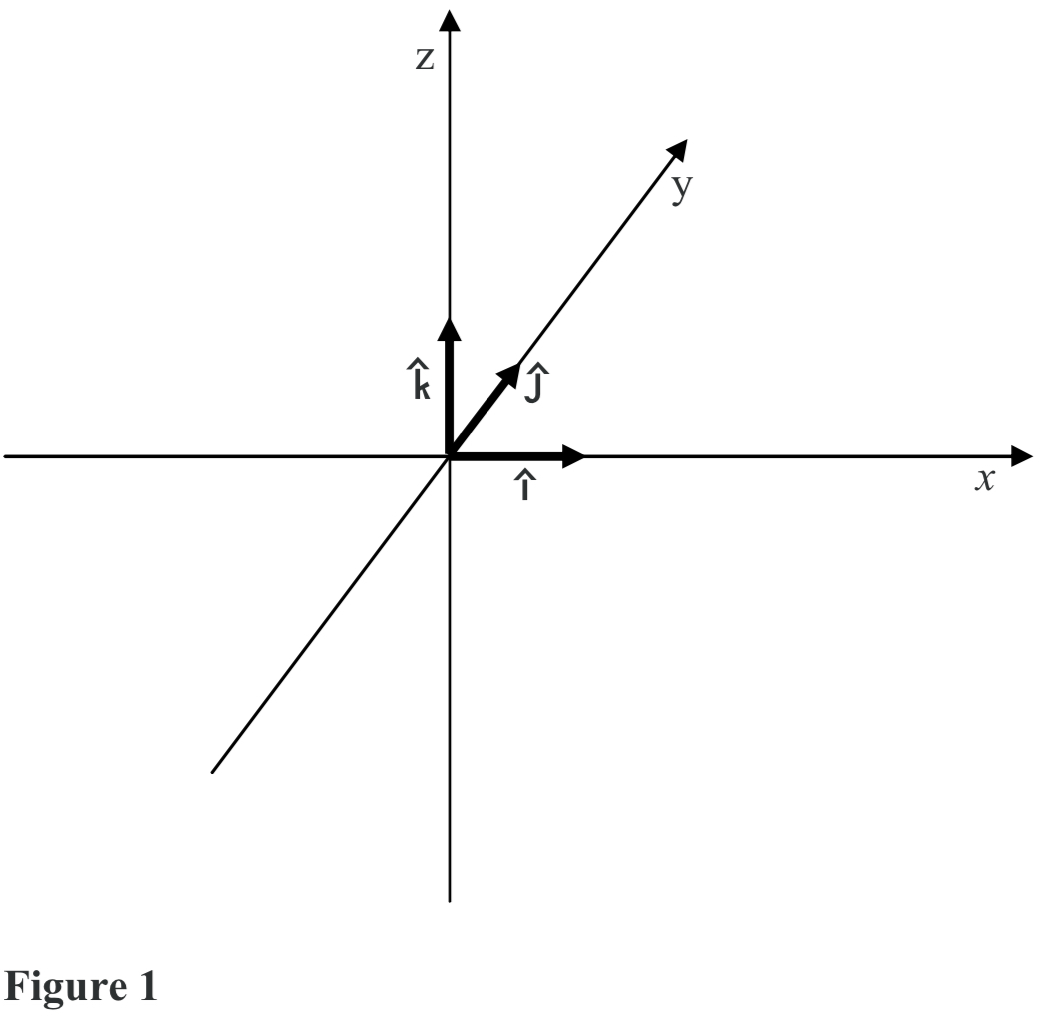
This is a second way to calculate the product of two vectors. It creates a third vector that is perpendicular to the plane made from the two vectors as shown in the figure [1].
The black arrow is perpendicular to the grey plane made from blue and red vectors). This is how you will find the amount of torque created from a force, which we will do many times. Also, unlike the dot product, a x b is a different direction than b x a.
$$ \vec A\times\vec B=\begin{bmatrix}
\underline{\hat{i}} & \underline{\hat{j}} & \underline{\hat{k}} \\
A_x & A_y & A_z \\
B_x & B_y & B_z
\end{bmatrix} $$
[latex]\vec {\textbf{A}}\times\vec{\textbf{B}}=(A_yB_z-A_zB_y)\underline{\hat{\textbf{i}}}+(A_zB_x-A_xB_z)\underline{\hat{\textbf{j}}}+(A_xB_y-A_yB_x)\underline{\hat{\textbf{k}}}[/latex]
[latex]|\vec {\textbf{A}}\times\vec {\textbf{B}}|=|\vec A||\vec B|\sin\theta[/latex]
The vector product of two vectors [latex]\vec A \text{ and }\vec B[/latex] is denoted by [latex]\vec A \text{ x }\vec B[/latex] and is often referred to as a cross product. The vector product is a vector that has its direction perpendicular to both vectors [latex]\vec A \text{ and }\vec B[/latex]. In other words, vector [latex]\vec A \text{ x }\vec B[/latex] is perpendicular to the plane that contains vectors [latex]\vec A \text{ and }\vec B[/latex].
Source: University Physics Volume 1, OpenStax CNX, https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/2-4-products-of-vectors/
Unit vectors allow for a straightforward calculation of the cross product of two vectors under even the most general circumstances, e.g. circumstances in which each of the vectors is pointing in an arbitrary direction in a three-dimensional space. To take advantage of the method, we need to know the cross product of the Cartesian coordinate axis unit vectors i, j, and k with each other. First off, we should note that any vector crossed into itself gives zero. This is evident from the equation:
[latex]|\vec A\times\vec B|=|\vec A||\vec B|\sin\theta[/latex].
because if A and B are in the same direction, then θ = 0°, and since sin 0° = 0, we have [latex]|\vec A\times\vec B|=0[/latex]. Regarding the unit vectors, this means that:
$$\underline{\hat{i}}\times\underline{\hat{i}}=0\\\underline{\hat{j}}\times\underline{\hat{j}}=0\\\underline{\hat{k}}\times\underline{\hat{k}}=0$$
Next we note that the magnitude of the cross product of two vectors that are perpendicular to each other is just the ordinary product of the magnitudes of the vectors. This is also evident from the equation:
$$|\vec {A}\times\vec{B}|=|\vec A||\vec B|\sin\theta$$
because if [latex]\vec A[/latex] is perpendicular to [latex]\vec B[/latex] then θ = 90° and sin90° = 1 so:
$$|\vec A\times\vec B|=|\vec A||\vec B|$$
Now if A and B are unit vectors, then their magnitudes are both 1, so, the product of their magnitudes is also 1. Furthermore, the unit vectors i, j, and k are all perpendicular to each other so the magnitude of the cross product of any one of them with any other one of them is the product of the two magnitudes, that is, 1.
Now how about the direction? Let’s use the right hand rule to get the direction of i×j:
[To find the direction, we use the right-hand rule which we will cover more in section 3.1. Here is an overview]. With the fingers of the right hand pointing directly away from the right elbow, and in the same direction as i, (the first vector in “[latex]\underline{\hat{i}}\times\underline{\hat{j}}[/latex]”) to make it so that if one were to close the fingers, they would point in the same direction as [latex]\underline{\hat{j}}[/latex], the palm must be facing in the +y direction. That being the case, the extended thumb must be pointing in the +z direction. Putting the magnitude (the magnitude of each unit vector is 1) and direction (+z) information together we see that:
- [latex]\underline{\hat{i}}\times\underline{\hat{j}}=\underline{\hat{k}}[/latex]
- [latex]\underline{\hat{j}}\times\underline{\hat{k}}=\underline{\hat{i}}[/latex]
- [latex]\underline{\hat{k}}\times\underline{\hat{i}}=\underline{\hat{j}}[/latex]
- [latex]\underline{\hat{j}}\times\underline{\hat{i}}=-\underline{\hat{k}}[/latex]
- [latex]\underline{\hat{k}}\times\underline{\hat{j}}=-\underline{\hat{i}}[/latex]
- [latex]\underline{\hat{i}}\times\underline{\hat{k}}=-\underline{\hat{j}}[/latex]
One way of remembering this is to write [latex]\underline{\hat{i}},\underline{\hat{j}},\underline{\hat{k}}[/latex] twice in succession:
[latex]\underline{\hat{\textbf{i}}},\underline{\hat{\textbf{j}}},\underline{\hat{\textbf{k}}},\underline{\hat{\textbf{i}}},\underline{\hat{\textbf{j}}},\underline{\hat{\textbf{k}}}[/latex]
Then, crossing any one of the first three vectors into the vector immediately to its right yields the next vector to the right. But crossing any one of the last three vectors into the vector immediately to its left yields the negative of the next vector to the left (left-to-right “+“, but right-to-left “−“).
Now we’re ready to look at the general case. Any vector [latex]\vec A[/latex] can be expressed in terms of unit vectors:
$$\vec{\textbf{A}}=A_x\hat{\underline{i}}+A_y\hat{\underline{j}}+A_z\hat{\underline{k}}$$
Doing the same for a vector [latex]\vec B[/latex] then allows us to write the cross product as:
$$\vec{\textbf{A}}\times\vec{\textbf{B}}=(A_x\hat{\underline{i}}+A_y\hat{\underline{j}}+A_z\hat{\underline{k}})\times(B_x\hat{\underline{i}}+B_y\hat{\underline{j}}+B_z\hat{\underline{k}})$$
Using the distributive rule for multiplication we can write this as:
$$\begin{aligned}\vec{\textbf{A}}\times\vec{\textbf{B}}=&A_x\hat{\underline{i}}\times(B_x\hat{\underline{i}}+B_y\hat{\underline{j}}+B_z\hat{\underline{k}})+\\&A_y\hat{\underline{j}}\times(B_x\hat{\underline{i}}+B_y\hat{\underline{j}}+B_z\hat{\underline{k}})+\\&A_z\hat{\underline{k}}\times(B_x\hat{\underline{i}}+B_y\hat{\underline{j}}+B_z\hat{\underline{k}})\end{aligned}$$
$$\begin{aligned}\vec{\textbf{A}}\times\vec{\textbf{B}}=&A_x\hat{\underline{i}}\times B_x\hat{\underline{i}}+A_x\hat{\underline{i}}\times B_y\hat{\underline{j}}+A_x\hat{\underline{i}}\times B_z\hat{\underline{k}}+\\&A_y\hat{\underline{j}}\times B_x\hat{\underline{i}}+A_y\hat{\underline{j}}\times B_y\hat{\underline{j}}+A_y\hat{\underline{j}}\times B_z\hat{\underline{k}}+\\&A_z\hat{\underline{k}}\times B_x\hat{\underline{i}}+A_z\hat{\underline{k}}\times B_y\hat{\underline{j}}+A_z\hat{\underline{k}}\times B_z\hat{\underline{k}}\end{aligned}$$
Using, in each term, the commutative rule and the associative rule for multiplication we can write this as:
$$\begin{aligned}\vec{\textbf{A}}\times\vec{\textbf{B}}=&A_xB_x(\hat{\underline{i}}\times\hat{\underline{i}})+A_xB_y(\hat{\underline{i}}\times\hat{\underline{j}})+A_xB_z(\hat{\underline{i}}\times\hat{\underline{k}})+\\&A_yB_x(\hat{\underline{j}}\times\hat{\underline{i}})+A_yB_y(\hat{\underline{j}}\times\hat{\underline{j}})+A_yB_z(\hat{\underline{j}}\times\hat{\underline{k}})+\\&A_zB_x(\hat{\underline{k}}\times\hat{\underline{i}})+A_zB_y(\hat{\underline{k}}\times\hat{\underline{j}})+A_zB_z(\hat{\underline{k}}\times\hat{\underline{k}})\end{aligned}$$
Now we evaluate the cross product that appears in each term:
$$\begin{aligned}\vec A\times\vec B=&A_xB_x(0)+A_xB_y(\underline{\hat{k}})+A_xB_z(-\underline{\hat{j}})+\\&A_yB_x(-\underline{\hat{k}})+A_yB_y(0)+A_yB_z(\underline{\hat{i}})+\\&A_zB_x(\underline{\hat{j}})+A_zB_y(-\underline{\hat{i}})+A_zB_z(0)\end{aligned}$$
Eliminating the zero terms and grouping the terms with i together, the terms with j together, and the terms with k together yields:
$$\begin{aligned}\vec A\times\vec B=&A_yB_z(\underline{\hat{i}})+A_zB_y(-\underline{\hat{i}})+\\&A_zB_x(\underline{\hat{j}})+A_xB_z(-\underline{\hat{j}})+\\&A_xB_y(\underline{\hat{k}})+A_yB_x(-\underline{\hat{k}})\end{aligned}$$
Factoring out the unit vectors yields:
$$\begin{aligned}\vec A\times\vec B=&(A_yB_z-A_zB_y)\underline{\hat{i}}+\\&(A_zB_x-A_xB_z)\underline{\hat{j}}+\\&(A_xB_y-A_yB_x)\underline{\hat{k}}\end{aligned}$$
which can be written on one line as:
$$\vec A\times\vec B=(A_yB_z-A_zB_y)\underline{\hat{i}}+(A_zB_x-A_xB_z)\underline{\hat{j}}+(A_xB_y-A_yB_x)\underline{\hat{k}}$$
This is our end result. We can arrive at this result much more quickly if we borrow a tool from that branch of mathematics known as linear algebra (the mathematics of matrices).
We form the 3×3 matrix:
$$ \begin{bmatrix}
\underline{\hat{i}} & \underline{\hat{j}} & \underline{\hat{k}} \\
A_x & A_y & A_z \\
B_x & B_y & B_z
\end{bmatrix} $$
by writing i, j, k as the first row, then the components of the first vector that appears in the cross product as the second row, and finally the components of the second vector that appears in the cross product as the last row. It turns out that the cross product is equal to the determinant of that matrix. We use absolute value signs on the entire matrix to signify “the determinant of the matrix.” So we have:
$$ \vec A\times\vec B=\begin{bmatrix}
\underline{\hat{i}} & \underline{\hat{j}} & \underline{\hat{k}} \\
A_x & A_y & A_z \\
B_x & B_y & B_z
\end{bmatrix} $$
To take the determinant of a 3×3 matrix you work your way across the top row. For each element in that row you take the product of the elements along the diagonal that extends down and to the right, minus the product of the elements down and to the left; and you add the three results (one result for each element in the top row) together. If there are no elements down and to the appropriate side, you move over to the other side of the matrix (see below) to complete the diagonal.
For the first element of the first row, the i, take the product down and to the right,
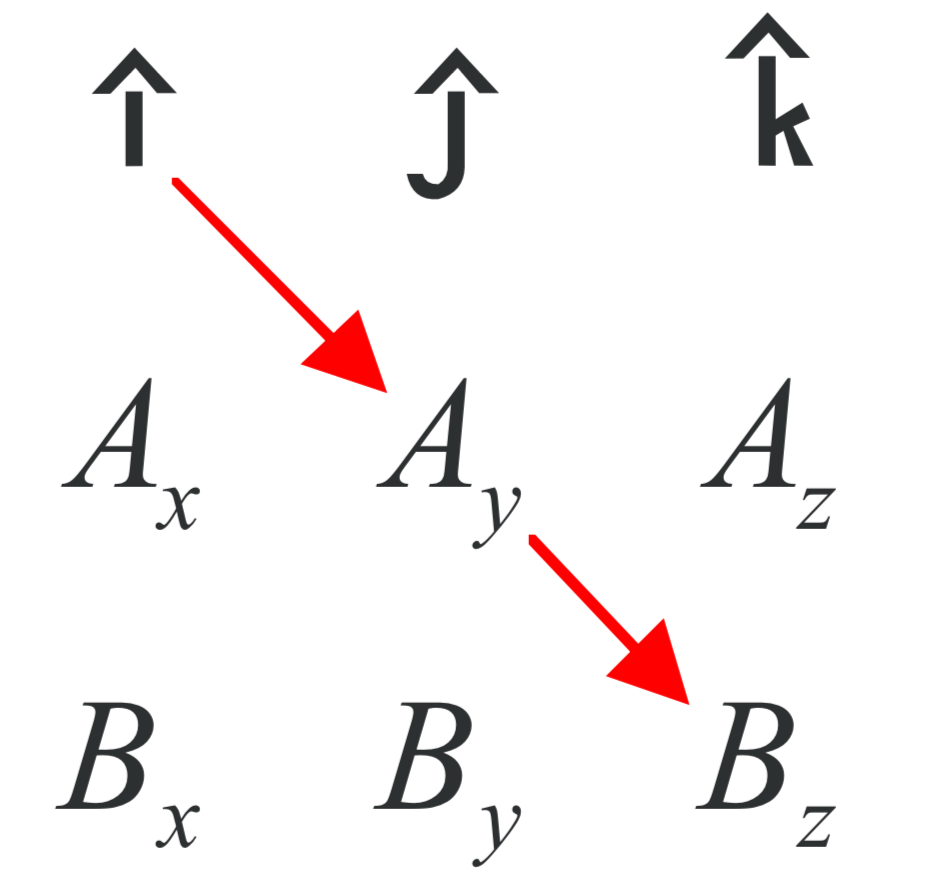
( this yields iAyBz) minus the product down and to the left
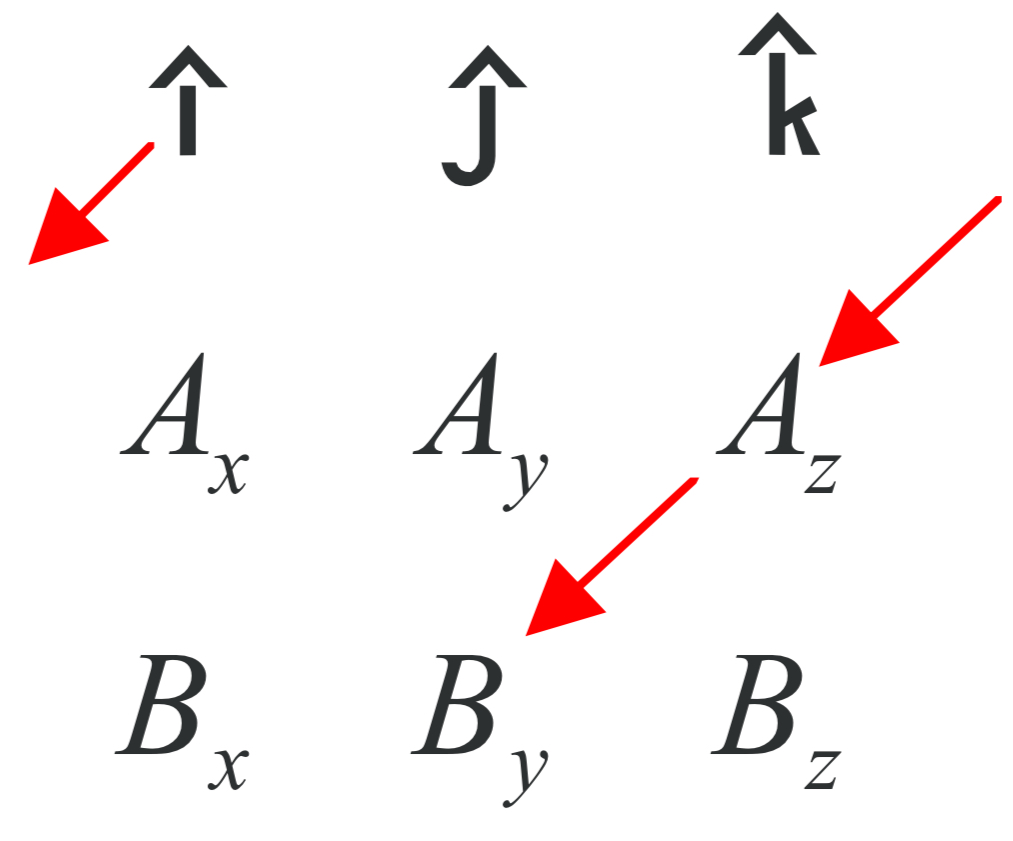
( the product down-and-to-the-left is iAzBy).
For the first element in the first row, we thus have: [latex]\underline{\hat{i}}[/latex]AyBz − [latex]\underline{\hat{i}}[/latex]AzBy which can be written as: (AyBz − AzBy)[latex]\underline{\hat{i}}[/latex]. Repeating the process for the second and third elements in the first row (the j and the k) we get (AzBx − AxBz)[latex]\underline{\hat{j}}[/latex] and (AxBy − AyBx)[latex]\underline{\hat{k}}[/latex] respectively. Adding the three results, to form the determinant of the matrix results in:
$$\vec A\times\vec B=(A_yB_z-A_zB_y)\underline{\hat{i}}+(A_zB_x-A_xB_z)\underline{\hat{j}}+(A_xB_y-A_yB_x)\underline{\hat{k}}$$
as we found before, “the hard way.” Below the diagram shows the direction of each part of the cross product:
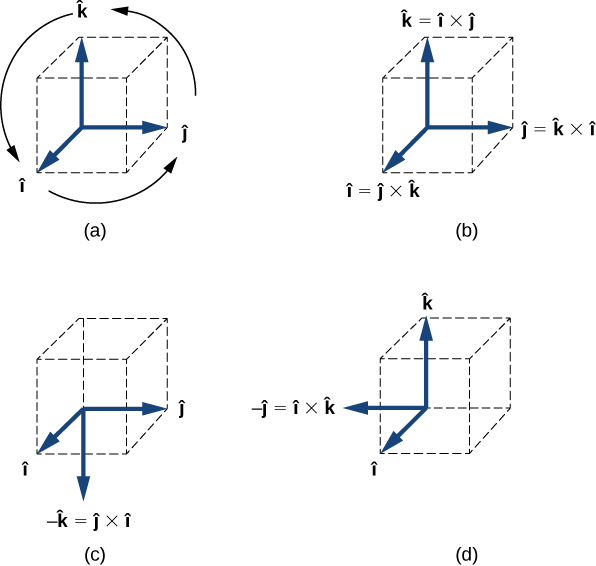
Source: Calculus Based Physics, Jeffrey W. Schnick, https://openlibrary.ecampusontario.ca/catalogue/item/?id=ce74a181-ccde-491c-848d-05489ed182e7 page 136–141
Key Takeaways
Basically: Cross product is a method to find a vector that is a product of two vectors, perpendicular to the plane created from the two vectors.
Application: While bicycling, the force of my foot pushing on the pedal produces the most rotation when the force is 90 degrees (perpendicular) from the surface of the pedal. The pedals themselves rotate so I can change the angle I am pushing with, otherwise when the pedal is at the bottom, it would be very difficult to produce forward motion.
Looking ahead: In the next section, 1.6 on Torque, we will use the cross product to find the moment produced from forces.

