Chapter 4: Rigid Bodies
4.1 External Forces
When we say ‘forces’ in Statics, we are generally talking about external forces (such as the reaction forces discussed in the previous chapter) and internal forces (that we will discuss in Chapters 5 and 6). Generally, external forces include:
- gravitational force (or weight)
- normal force
- frictional force
- spring force
- applied force (such as reaction forces & tension) – this also includes applied moments, such as from motors
In science class, you probably learned about the fundamental forces of nature: gravitational, electromagnetic, weak and strong nuclear forces. Normal force, friction, spring, and applied forces are all types of electromagnetic forces. The charged and neutral particles attract or repel each other. For example, the reason your laptop doesn’t fall through the table is that the electrons in the atoms of the two objects are repelling each other, and both objects are being pulled down by another fundamental force: gravitational force. See this page for more information. The four fundamental forces are beyond the scope of this Statics class, but it’s important to know the background on how the external forces operate. In this class, we’ll use our understanding of the external forces to learn how to quantify the forces and calculate the value of other forces.
- Gravity: Fg = mg
- Normal: Calculated
- Friction: Ff = mN
- Spring: FS = -kx
- Applied: Measured or calculated
Forces are given many names, such as push, pull, thrust, and weight. Traditionally, forces have been grouped into several categories and given names relating to their source, how they are transmitted, or their effects. Several of these categories are discussed in this section.
Normal Force
Weight (also called the force of gravity) is a pervasive force that acts at all times and must be counteracted to keep an object from falling. You must support the weight of a heavy object by pushing up on it when you hold it stationary. But how do inanimate objects like a table support the weight of a mass placed on them, such as shown in the figure below? When the bag of dog food is placed on the table, the table sags slightly under the load. This would be noticeable if the load were placed on a card table, but even a sturdy oak table deforms when a force is applied to it. Unless an object is deformed beyond its limit, it will exert a restoring force much like a deformed spring (or a trampoline or diving board). The greater the deformation, the greater the restoring force. Thus, when the load is placed on the table, the table sags until the restoring force becomes as large as the weight of the load. At this point, the net external force on the load is zero. That is the situation when the load is stationary on the table. The table sags quickly and the sag is slight, so we do not notice it. But it is similar to the sagging of a trampoline when you climb onto it.
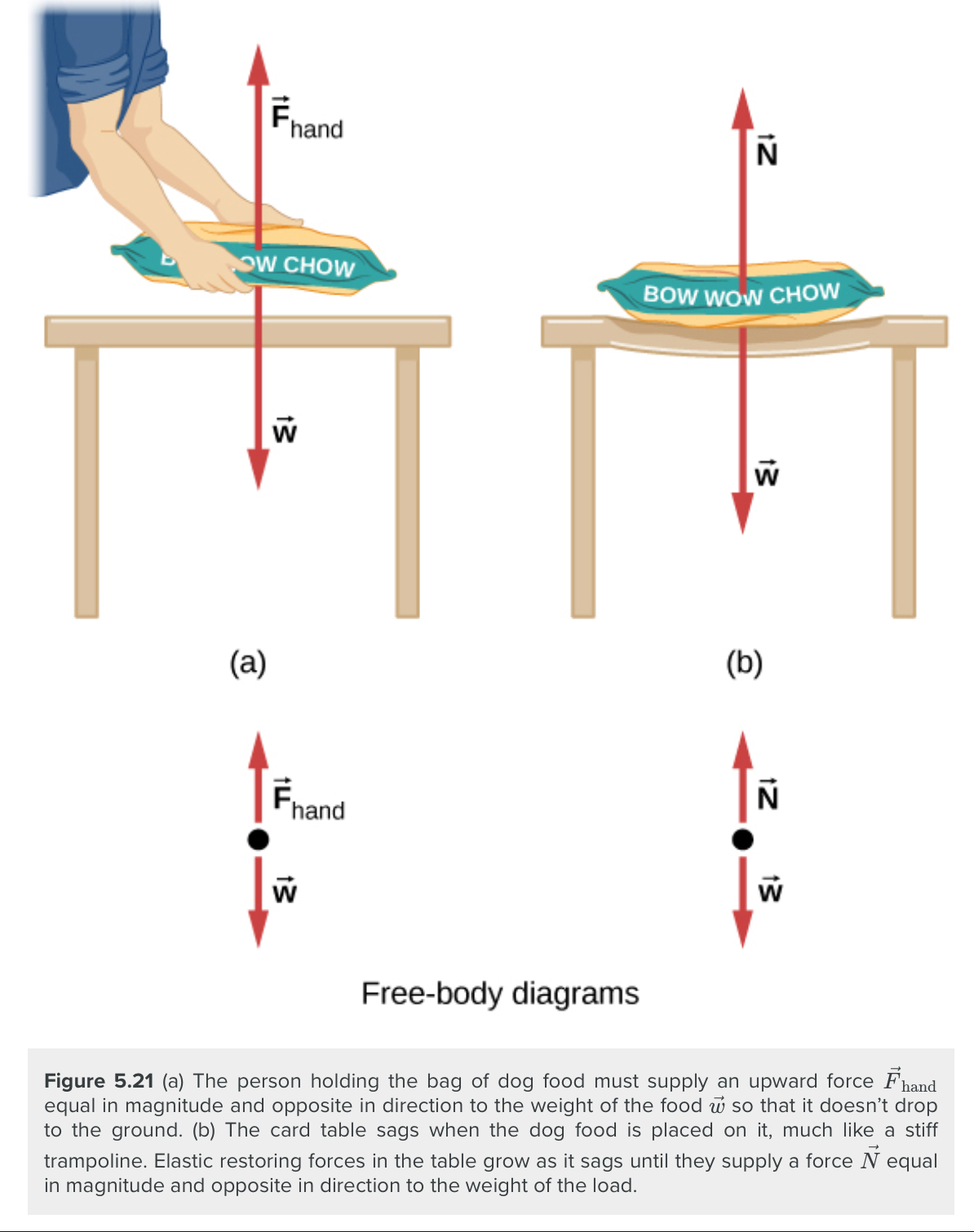
We must conclude that whatever supports a load, be it animate or not, must supply an upward force equal to the weight of the load, as we assumed in a few of the previous examples. If the force supporting the weight of an object, or a load, is perpendicular to the surface of contact between the load and its support, this force is defined as a normal force and here is given by the symbol [latex]\vec N[/latex] (This is not the newton unit for force, N.) The word normal means perpendicular to a surface. This means that the normal force experienced by an object resting on a horizontal surface can be expressed in vector form as follows:
$$\vec N=-m\vec g$$
In scalar form, this becomes:
$$N=mg$$
The normal force can be less than the object’s weight if the object is on an incline.
When an object rests on an incline that makes an angle θ with the horizontal, the force of gravity acting on the object is divided into two components: a force acting perpendicular to the plane, wy, and a force acting parallel to the plane, wx. The normal force [latex]\vec N[/latex] is typically equal in magnitude and opposite in direction to the perpendicular component of the weight wy. The force acting parallel to the plane, wx, causes the object to accelerate down the incline.
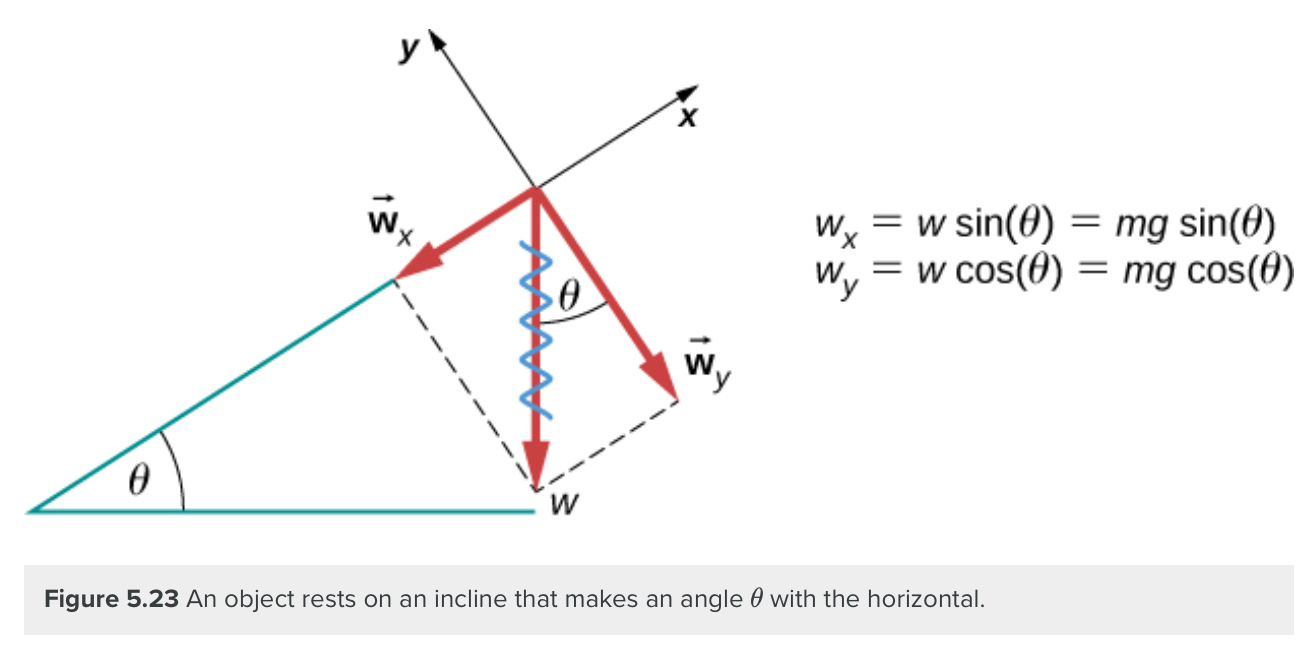
Be careful when resolving the weight of the object into components. If the incline is at an angle θ to the horizontal, then the magnitudes of the weight components are:
$$w_x=w\sin\theta=mg\sin\theta$$
and
$$w_y=w\cos\theta=mg\cos\theta$$
We use the second equation to write the normal force experienced by an object resting on an inclined plane:
$$N=mg\cos\theta$$
Instead of memorizing these equations, it is helpful to be able to determine them from reason. To do this, we draw the right angle formed by the three weight vectors. The angle θ of the incline is the same as the angle formed between w and wy. Knowing this property, we can use trigonometry to determine the magnitude of the weight components:
$$\cos\theta=\frac{w_y}{w},\:w_y=w\cos\theta=mg\cos\theta\\\sin\theta=\frac{w_x}{w},\:w_x=w\sin\theta=mg\sin\theta$$
Tension
A tension is a force along the length of a medium; in particular, it is a pulling force that acts along a stretched flexible connector, such as a rope or cable. The word “tension” comes from a Latin word meaning “to stretch.” Not coincidentally, the flexible cords that carry muscle forces to other parts of the body are called tendons.
Any flexible connector, such as a string, rope, chain, wire, or cable, can only exert a pull parallel to its length; thus, a force carried by a flexible connector is a tension with a direction parallel to the connector. Tension is a pull in a connector. Consider the phrase: “You can’t push a rope.” Instead, tension force pulls outward along the two ends of a rope.
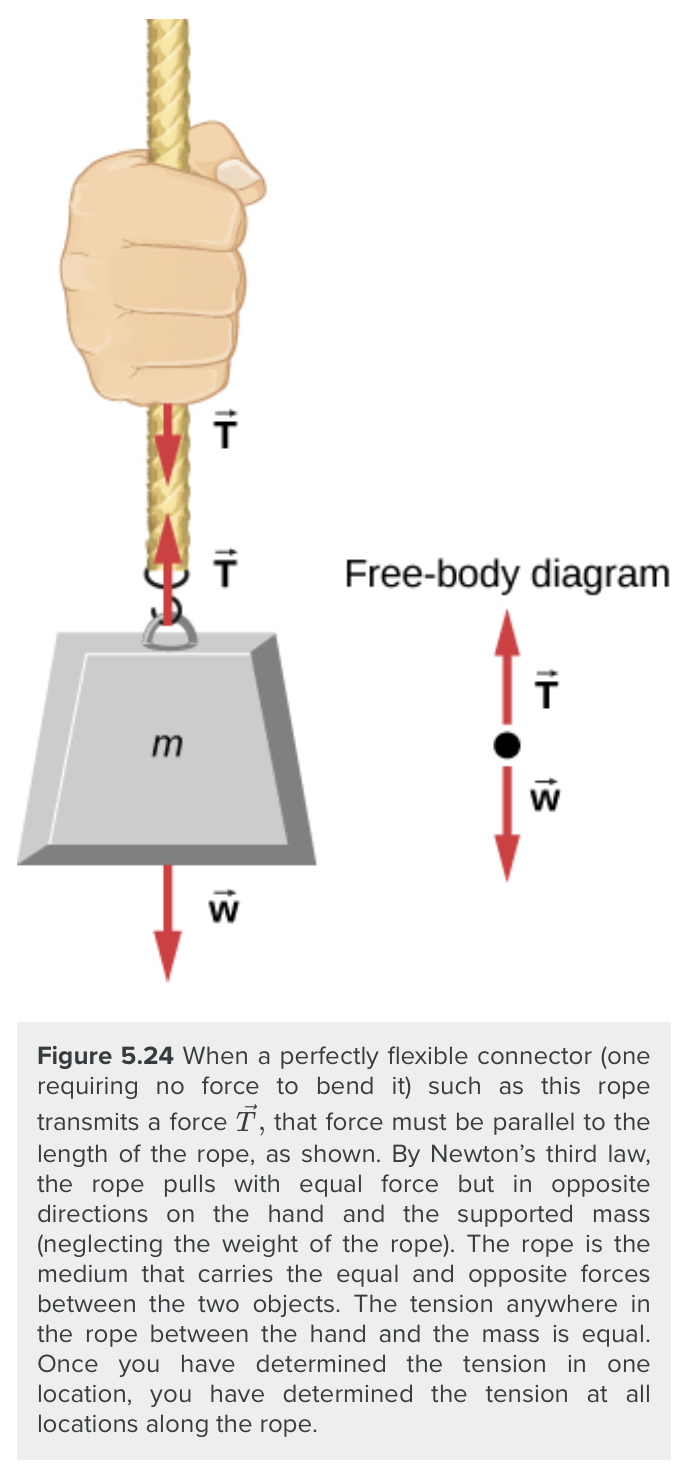
Consider a person holding a mass on a rope. If the 5.00-kg mass in the figure is stationary, then its acceleration is zero and the net force is zero. The only external forces acting on the mass are its weight and the tension supplied by the rope. Thus,
If we cut the rope and insert a spring, the spring would extend a length corresponding to a force of 49.0 N, providing a direct observation and measure of the tension force in the rope.
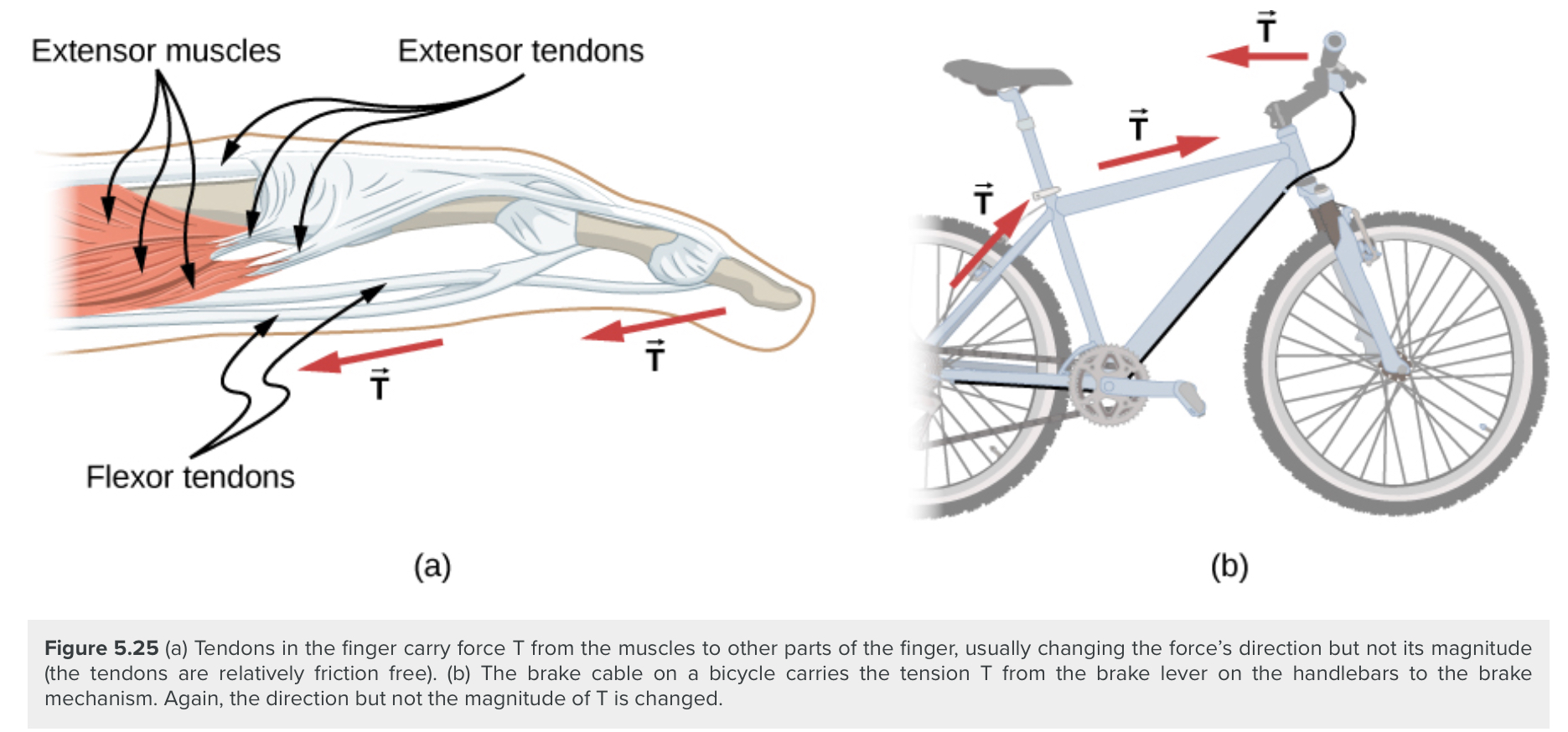
Flexible connectors are often used to transmit forces around corners, such as in a hospital traction system, a tendon, or a bicycle brake cable. If there is no friction, the tension transmission is undiminished; only its direction changes, and it is always parallel to the flexible connector, as shown below:
If we wish to create a large tension, all we have to do is exert a force perpendicular to a taut flexible connector. We can see that the tension in the rope is related to the force acting perpendicularly in the following way:
$$T=\frac{w}{2\sin\theta}$$
We can extend this expression to describe the tension T created when a perpendicular force (F⊥) is exerted at the middle of a flexible connector:
$$T=\frac{F\perp}{2\sin\theta}$$
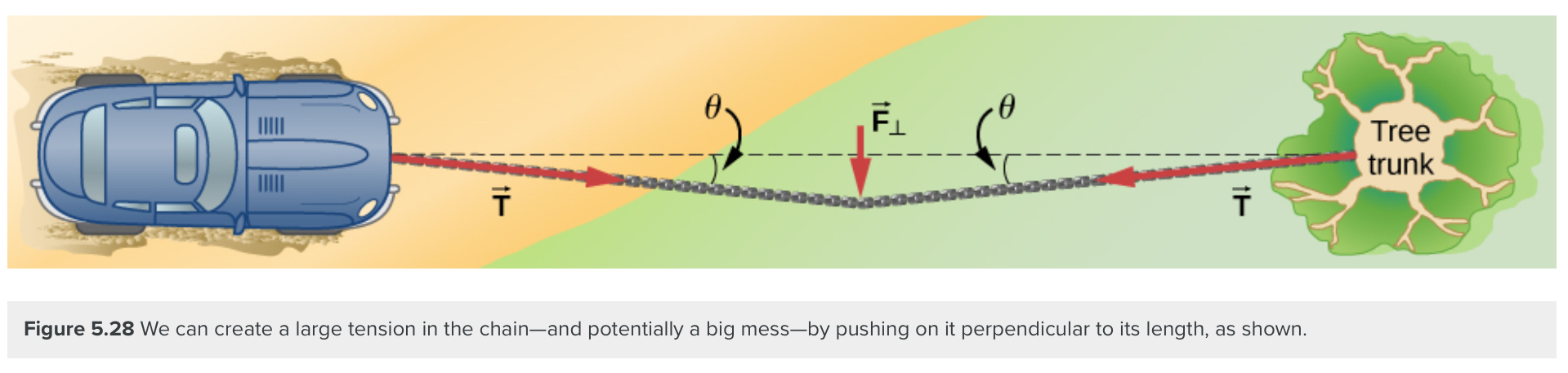
The angle between the horizontal and the bent connector is represented by θ. In this case, T becomes large as θ approaches zero. Even the relatively small weight of any flexible connector will cause it to sag, since an infinite tension would result if it were horizontal (i.e., θ=0 and sin θ=0). For example, the image below shows a situation where we wish to pull a car out of the mud when no tow truck is available. Each time the car moves forward, the chain is tightened to keep it as straight as possible. The tension in the chain is given by[latex]T=\frac{F\perp}{2\sin\theta}[/latex] and since θ is small, T is large. This situation is analogous to the tightrope walker, except that the tensions shown here are those transmitted to the car and the tree rather than those acting at the point where F⊥ is applied.
Friction
Friction is a resistive force opposing motion or its tendency. Imagine an object at rest on a horizontal surface. The net force acting on the object must be zero, leading to equality of the weight and the normal force, which act in opposite directions. If the surface is tilted, the normal force balances the component of the weight perpendicular to the surface. If the object does not slide downward, the component of the weight parallel to the inclined plane is balanced by friction. Friction is discussed in greater detail in the next chapter.
Spring Force
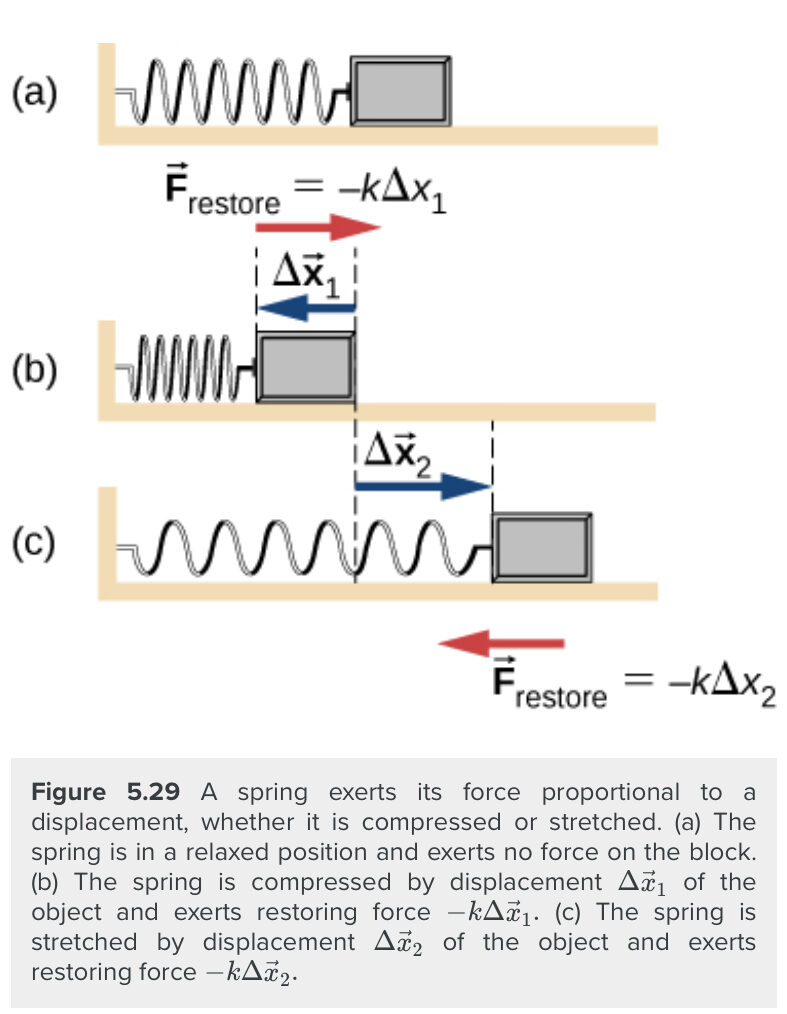
A spring is a special medium with a specific atomic structure that has the ability to restore its shape, if deformed. To restore its shape, a spring exerts a restoring force that is proportional to and in the opposite direction in which it is stretched or compressed. This is the statement of a law known as Hooke’s law, which has the mathematical form
$$\vec F=-k\vec x$$
The constant of proportionality k is a measure of the spring’s stiffness. The line of action of this force is parallel to the spring axis, and the sense of the force is in the opposite direction of the displacement vector. The displacement must be measured from the relaxed position; x=0 when the spring is relaxed.
Key Takeaways
- Basically: External forces include: gravitational, applied, normal, frictional, and spring.
- Application: Everything. A book on a table, Tigger bouncing on his tail, a shooting star, and a soccer ball rolling into the goal.
- Looking Ahead: Ch 5 and 6 will look at internal forces. Section 4.3 will use the known forces to calculate the unknown forces. Section 4.2 will model the forces on a diagram.

