Chapter 4: Rigid Bodies
4.5 Examples
Here are examples from Chapter 4 to help you understand these concepts better. These were taken from the real world and supplied by FSDE students in Summer 2021. If you’d like to submit your own examples, please send them to the author eosgood@upei.ca.
Example 4.5.1: External Forces, submitted by Elliott Fraser
1. Problem
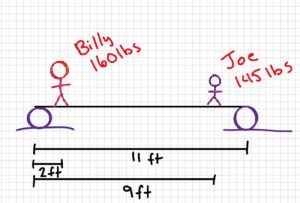
Billy (160 lbs), Bobby (180 lbs), and Joe (145 lbs) are walking across a small bridge with a length of 11 feet. Both sides of the bridge are supported by rollers. Billy is 2 feet along the bridge whereas Joe is 9 feet along the bridge. If the maximum force that the left side of the bridge can withstand without failing is 225 lbs, where along the bridge can Bobby stand?
Real-life scenario:

2.Draw
Sketch:
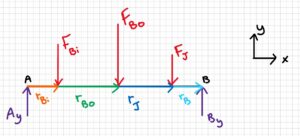
Free-body diagram:
3. Knowns and Unknowns
Knowns:
- rBi = 2 ft
- rJ = 9 ft
- rB = 11 ft
- FBi = 160 lb
- FJ = 145 lb
- FBo = 180 lb
- Ay = 225 lb (since this is the maximum force without failure)
Note: Since the mass of the bridge was not given, we assume it is negligible and ignore it for this question.
Unknown:
- rBo
4. Approach
Use equilibrium equations ( [latex]\sum\underline{F}=0[/latex] , [latex]\sum\underline{M}=0[/latex] ) . Use sum of forces in y to find By; use sum of moments to find where Bobby can stand. Solve for x.
5. Analysis
$$ \sum F_y=0=-F_{Bi}-F_{Bo}-F_J+A_y+B_y\\\\B_y=F_{Bi}+F_{Bo}+F_J-A_y\\\\B_y=160 lb+180 lb+145 lb-225 lb\\\\\\B_y=260 lb$$
$$\sum M_A=0=-(F_{Bi})(r_{Bi})-(F_{Bo})(r_{Bo})-(F_{J})(r_{J})+(B_{y})(r_{B})\\r_{bo}=\frac{-(F_{Bi})(r_{Bi})-(F_{J})(r_{J})+(B_{y})(r_{B})}{F_{Bo}}\\r_{Bo}=\frac{-(160 lb)(2 ft)-(145 lb)(9 ft)+(260 lb)(11 ft)}{180 lb}$$
$$\underline{r_{Bo}=6.86 ft}$$
6. Review
Bobby can stand anywhere from 6.8611 ft – 11 ft from A with no problems. If Bobby were to stand between 0 ft and 6.811 ft, the left side of the bridge would fail.
Example 4.5.2: Free-Body Diagrams, submitted by Victoria Keefe
1. Problem
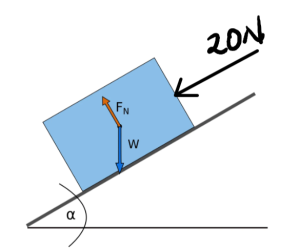 Source:https://www.omnicalculator.com/physics/normal-force
Source:https://www.omnicalculator.com/physics/normal-force2. Draw
3. Knowns and Unknowns
Knowns:
- θ = 15°
- FA
Unknown:
- Free-body diagram of box
4. Approach
Draw the box, then draw all forces acting on it
5. Analysis
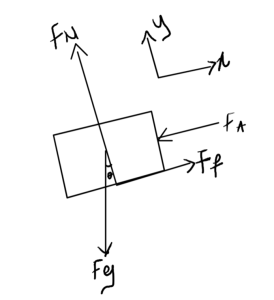
6. Review
All forces acting upon the box are drawn, including weight/gravitational force, normal force, friction, and applied forces.
Example 4.5.3: Friction, submitted by Deanna Malone
1. Problem
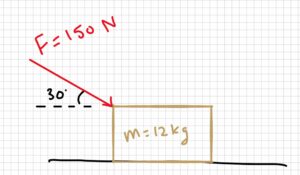
A box is being pushed along level ground with a force of 150 N at an angle of 30° with the horizontal. The mass of the box is 12 kg.
a) What is the normal force between the box and the floor?
b) What is the coefficient of friction between the box and the floor?
2. Draw
Sketch:
Free Body Diagram:
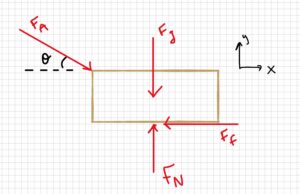
3. Knowns and Unknowns
Knowns:
- FA = 150 N
- θ = 30°
- m = 12 kg
Unknowns:
- FN
- μ
4. Approach
Use equilibrium equations ( [latex]\sum\underline{F}=0[/latex] , [latex]\sum\underline{M}=0[/latex] ), SOH CAH TOA, friction equation
5. Analysis
Part a:
Find Fg:
$$Fg=m\cdot g\\Fg=(12kg)(9.81m/s^2)\\\\Fg=117.72N$$
Find FN using equilibrium equations:
$$\sum Fy=0=F_N-F_g-F_A\sin 30^{\circ}\\0=F_N-117.72N-150N\cdot \sin 30^{\circ}\\F_N=117.72+150N\cdot\sin 30^{\circ}\\\\\underline{F_N=192.7 N}$$
Part b:
Find two equations for Ff, set them equal to each other, and solve for μ
\begin{align*}
\sum F_x &= 0 = F_A \cos 30^\circ – F_f \\
0 &= 150\,N \cdot \cos 30^\circ – F_f
\end{align*}
$$
$$F_f=150N\cdot\cos 30^{\circ}\\F_f=\mu\cdot F_N\\150N\cdot\cos 30^{\circ}=\mu\cdot F_N$$
$$\mu=\frac{150N\cdot\cos 30^{\circ}}{F_N}\\\mu=\frac{150N\cdot\cos 30^{\circ}}{192.72N}=0.67405$$
$$\underline{\mu=0.67}$$
6. Review
FN, Fg, and the y component of FA are the only forces in the y direction so it makes sense that they need to equal zero for the equilibrium equations. FN is the only positive force in the y direction, so it makes sense that it equals the magnitude of the other two put together.
The coefficient found between the box and the floor is reasonable as it is less than 1, and it’s reasonable for a box on the floor. For example, if the box was wood and the floor was wood, the coefficient of static friction would be anywhere from 0.5-0.7, so having a coefficient of friction being equal to 0.67 makes sense.
Example 4.5.4: Friction, submitted by Dhruvil Kanani
1. Problem
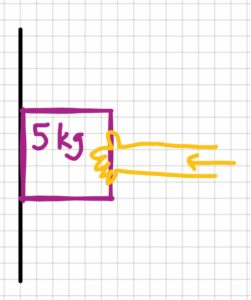
A person is trying to prevent a brick from sliding on a rough vertical surface by applying force in the direction of wall. Assuming the coefficient of static friction is 0.49 and mass of the brick is 5 kg,
- a) Determine the minimum force required to prevent the brick from slipping.
- b) Find the distributed load or intensity if the length of the person’s hands from the tip of his fingers to their wrist is 16 cm.
2. Draw
Sketch:
Free-body diagram (box):
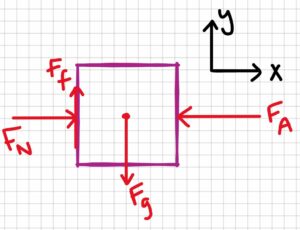
Free-body diagram (distributed load):
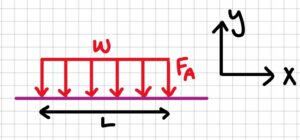
3. Knowns and Unknowns
Knowns:
- Mass of brick (m) = 5kg
- Coefficient of friction (μ1) = 0.49
- Acceleration due to gravity (g) = 9.81m/s2
- Length of the hand (L) = 16 cm
Unknowns:
- Applied force (FA)
- Intensity (w)
4. Approach
Use equilibrium equations ( [latex]\sum\underline{F}=0[/latex] , [latex]\sum\underline{M}=0[/latex] ), equations for Fg and Ff (see below).
$$F_g=m g\\F_f=\mu F_N$$
5. Analysis
Part a:
$$F_g=m\cdot g\\F_g=5kg\cdot 9.81m/s^2\\F_g=49.05N$$
$$\sum F_y=0=-F_g+F_f\\F_f=F_g\\F_f=49.05N$$
$$F_f=\mu_1 F_N\\F_N=\frac{F_f}{\mu_1}\\F_N=\frac{49.05N}{0.49}$$
$$\underline{F_N=100.1N}$$
Part b:
$$\sum F_x=0=F_N-F_A\\F_A=F_N\\F_A=100.1N$$
$$w=\frac{F_A}{L}\\w=\frac{100.1N}{(16cm\times\frac{1m}{100cm})}$$
$$\underline{w=625.64N/m}$$
6. Review
It makes sense that the applied force is larger than the gravitational force. It also makes sense that the normal and applied forces are equal, since they are the only forces in the x direction (same goes for the friction and gravitational forces).
Example 4.5.5: Friction, submitted by Emma Christensen
1. Problem
A ball is suspended by two ropes and rests on an inclined surface at an angle of 15°. Rope A pulls on the ball with a force of 200 N, and rope B has a force of 150 N. They each have angles of 20° and 60°, respectively, from the inclined surface plane, as shown in the image below.
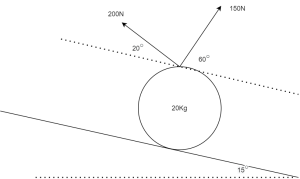
a) Draw a free-body diagram of the ball
b) Find the friction force
2. Draw
Sketch:

3. Knowns and Unknowns
- θA = 20°
- θB = 60°
- θC = 15°
- m = 20 kg
- FA = 200 N
- FB = 150 N
Unknown:
- Ff
4. Approach
Draw the ball, then add forces. Use equilibrium equations ( [latex]\sum\underline{F}=0[/latex] , [latex]\sum\underline{M}=0[/latex] ) to find the friction force.
5. Analysis
Part a:
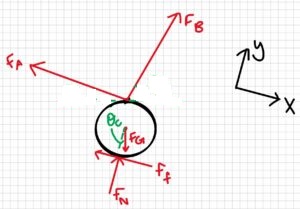
Part b:
Step 1: find FG
$$F_G=m g\\F_G=20kg\cdot 9.81m/s^2\\F_G=196.2N$$
Step 2: Find the x-component of FG
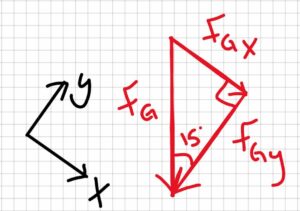
$$F_{GX}=F_G\sin(15^{\circ})\\F_{GX}=196.2N\cdot\sin(15^{\circ})\\F_{GX}=50.78N$$
Step 3: Find the x-component of FA
$$\cos(20^{\circ})=\frac{F_AX}{F_{A}}\\F_{AX}=F_A\cdot(cos(20^{\circ}))\\F_{AX}=200N\cdot(\cos(20^{\circ}))\\F_{AX}=187.938N$$
Step 4: Find the x-component of FB
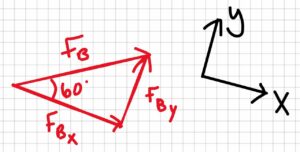
$$F_{BX}=F_B\cdot(\cos(60^{\circ}))\\F_{BX}=150N\cdot(\cos(60^{\circ}))\\F_{BX}=75N$$
Step 5: Sum forces in the x-direction to find the frictional force
$$\sum F_x=0=-F_f+F_{BX}-F_{AX}+F_{GX}\\F_f=-F_{AX}+F_{BX}+F_{GX}\\F_f=-187.938N+75N+50.78N$$
$$\underline{F_f=-62.158N}$$
Because the frictional force is negative, that means the frictional force actually acts in the opposite direction, so the friction is keeping the ball from going up the plane.
6. Review
The units of Ff are newtons, which makes sense because it is a force. It also makes sense that FAx is larger than FGx and FBx.
Example 4.5.6: Friction, Submitted by Riley Fitzpatrick
- Problem
A 6m trailer contains 500 kg that is distributed evenly across its bed, meaning that the weight of the load is acting at the centroid. The trailer has an axle at either end of the bed and a 3m hitch. A truck is towing the load with a force of 5000N.
a. Calculate the weight of the load.
b. Calculate the total normal force acting on the wheels.
c. Calculate the frictional force acting on the wheels.
d. Calculate the coefficient of friction between the wheels and the asphalt.
e. Given that the static coefficient of friction between the wheels and the asphalt is 0.72. Is the trailer about to slip?

An image relatable to the the problem. https://en.wikipedia.org/wiki/Sidelifter#/media/File:Sidelifter_in_forest.jpg
2. Draw
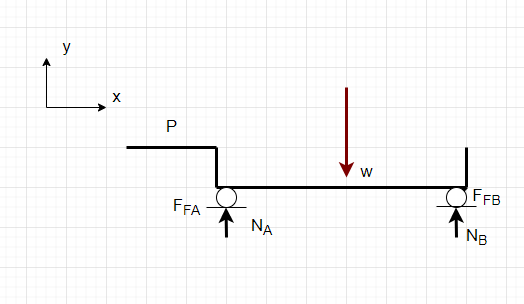
3.Knowns and Unknowns
Knowns:
- m = 500 kg
- P = 5000 N
- 9 = 9.81 m/s^2
Unknowns:
- w
- N
- FF
- µ
4. Approach
- Calculate w using the formula w = mg
- Calculate N using [latex]\sum{F_{y}} = 0[/latex]
- Calculate FF using [latex]\sum{F_{x}} = 0[/latex]
- Calculate µ using [latex]\mu= \dfrac{F_{F}}{N}[/latex]
- Compare µ to µs
5. Analysis
Calculating w
[latex]w = m\cdot g[/latex]
[latex]\:\:\:=500kg \cdot 9.81 m/s^2 = 4905 N[/latex]
w = 4905 N
Calculating N
[latex]\sum {F_y} = N-w =0[/latex]
[latex]N=w[/latex]
N = 4905 N
Therefore, NA = NB = 4905N/2 = 2452.5N
Finding FF
[latex]\sum {F_x}= P-F_{F} = 0[/latex]
[latex]P = F_{F}[/latex]
FF = 5000 N
Finding µ
[latex]\mu = \dfrac {F_{F}}{N} = \dfrac{5000 N }{4905 N}[/latex]
µ = 1.019
Comparing µ and µs
1.019> 0.72
µ > µs
Thus, the trailer is is in motion, i.e. sliding along the surface.
6. Review
From initial inspection of the FBD, it is clear that w (acting downwards) is opposite to the normal forces (acting upwards). The sum of the normal forces would not exceed w.
FF should be equal and opposite to P.
Example 4.5.7: Slip or Tip, submitted by Luke McCarvill
- Problem
1.8 metres tall Spiderman with strong spider-like webs is attempting to tip over a 10 m tall and 2.5 m wide shipping container sitting upright. Given that the coefficient of static friction between the bottom of the shipping container and the ground is 0.2, and the mass of the container is 2000 kg, how much tension must Spiderman impart on his web in order to barely tip over the container towards him if he is 20 metres away from the bottom of the container?
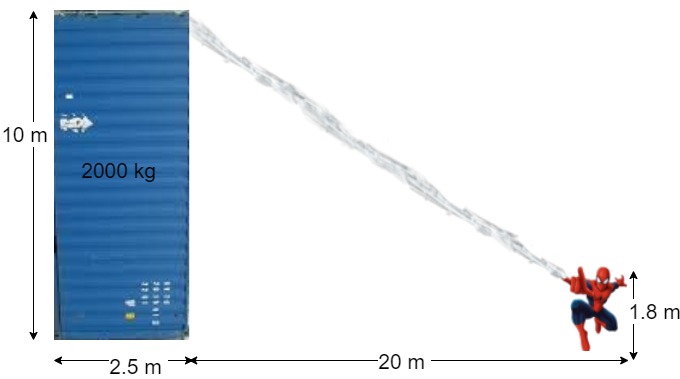
source:https://commons.wikimedia.org/wiki/File:Container_%E3%80%90_22G1_%E3%80%91_GVTU_201551(1)_%E3%80%90_Container_pictures_taken_in_Japan_%E3%80%91.jpg
2. Draw
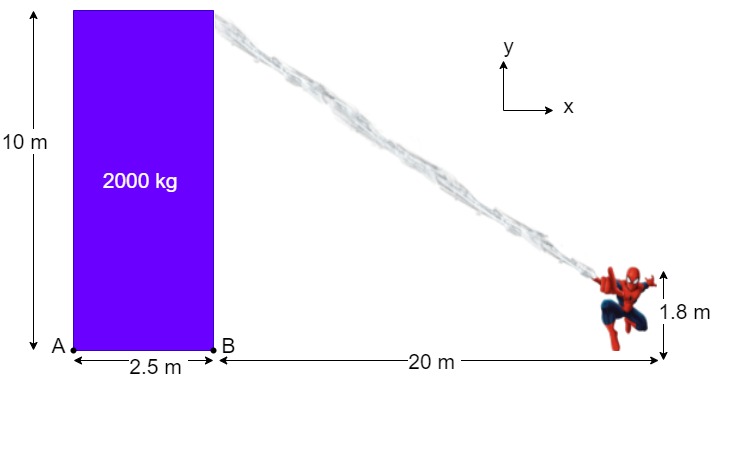
3. Knowns and Unknowns
Knowns:
- m = 2000 kg
- hc = 10 m
- hs = 1.8 m
- d = 20 m
- w =2.5
- μ = 0.2
Unknowns:
- Tx
- Ty
4. Approach
Componentizing forces in the x-y direction and using the summation of moments and forces to be equal to zero.
5. Analysis
Because mass is given force by gravity, [latex]F_{g }= m\times g=19,620 N[/latex]
Since the tension applied by Spider-Man is a force with both x and y components, we would need angle [latex]\theta[/latex]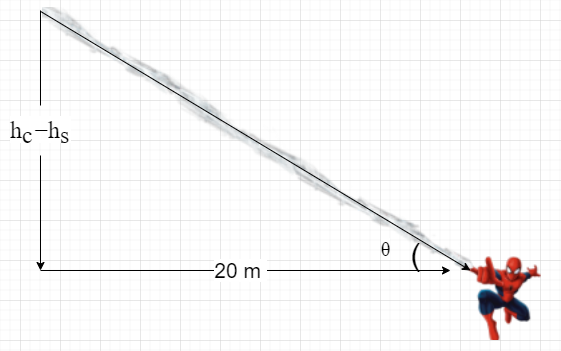
[latex]\theta = \tan^{-1} \left( \frac{h_c - h_s}{20} \right) = 22.3^\circ[/latex]
Analyzing the force diagram:
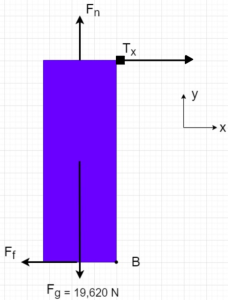
Looking at the force diagram for the shipping container, it is understood that if the container were to tip towards Spiderman, the sum of moments on point B would equal zero. It is noticeable that among the forces on the container( frictional force, normal force, force of gravity, and tension) only force of gravity and x component of tension contribute to the moment at point B. Therefore, the following equation for the moment at B is derived.
[latex]M_{B} =\: -h_{c}\times T_{x}+\frac{w}{2}\times F_{g} \:=0\\ \kern 1pc =10m \times T_{x}+\frac{2.5}{2}\times 19,620 N[/latex]
thus, [latex]T_{x} = 2,452.5 N[/latex]
Also
[latex]T_{x} = T\cos{\theta}[/latex]
[latex]\lvert T\rvert = \frac{T_{x}}{\cos{\theta}}=2,651 N[/latex]
The required tension to tip the container is 2,651 N
6. Review
We can ensure that the container will tip, not slip, by examining the role of frictional force in the net force. If the maximum frictional force is greater than the pulling force, the container would tip. To verify this, we analyze the below given force diagram to find the frictional force.
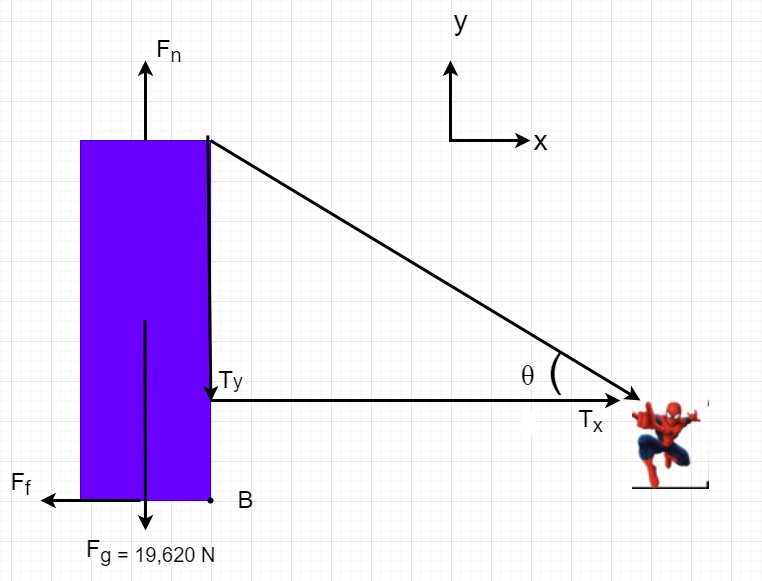
[latex]\begin{aligned} F_y &= -T_y + F_n - F_g \\ 0 &= -T \sin{\theta} + F_n - F_g \\ 0 &= -2651 \cdot \sin{22.3^\circ} + F_n - 19620 \\ F_n &= 20626\,N \end{aligned}[/latex]
now [latex]F_{f}=\mu \times F_{n} \\ F_{f} = 4,125 N[/latex]
Because Ff > Tx, the container will tip.
Example 4.5.8: Friction, submitted by Michael Oppong-Ampomah
- Problem
Find the frictional force between the ramp and the cart of mass 70 kg. A person pulls the cart with a rope with a tension of 300 N, and the ramp is tilted 30 degrees.

A relatable scenario as given in the problem. https://en.wikipedia.org/wiki/Baggage_handler#/media/File:BaggageHandlerDetroit7August2006.png
2. Draw 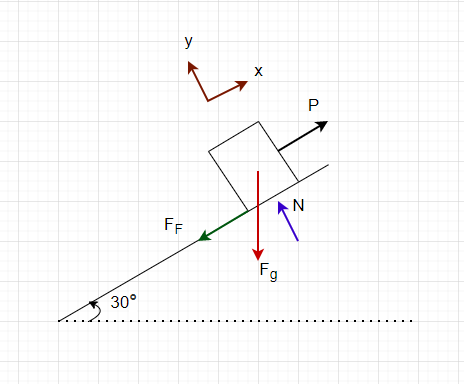
3. Knowns and Unknowns
Knowns:
- m= 70 kg
- P = 300N
- θ = 30°
Unknowns:
- Fg
- FF
4. Approach
- Find Fg by using Fg = m⨯g.
- Figuring out forces in x and y components
- Apply equilibrium equation to figure out the rest of the forces.
5. Analysis
Finding Fg
[latex]F_{g} = m \cdot g = 70 kg \cdot 9.81m/s^2 = 686.7 N[/latex]
Forces in x and y components
Since P, FF, and N are in the direction of either x or y, only Fg has a x and y components.
[latex]F_{gx} =686.7\cdot \sin{30}[/latex]
[latex]F_{gx} =343.35N[/latex]
Equilibrium equation in x-axis
∑Fx = 300N – FF− 686.7N sin(30°) = 0
FF=-43.35N
Since this value is negative it just means that the drawing has the force of friction acting in the opposite direction.
6. Review
The answer obtained makes sense as the force of friction should be small and be working against the cart sliding down the incline. The force of gravity in the x component is only slightly larger than that of the person pulling the cart so the force of friction being only 43.35N makes sense.
Example 4.5.9: Finding the coefficient of friction by Liam Murdock
1. Problem
You are developing an accessible gaming platform for a charity to allow everyone to play their favourite games.

The platform can be simplified for the calculations into a box 0.8 m long and 0.15m high. The platform has a mass of 4 kg and rests on the two thighs of a person each 0.2m wide and each 0.1 m away from the edges of the platform. Say the charity would want to make sure that a force of 10 N (from any of the top corners of the platform, going parallel to the surface) will not push it over. Make proper assumptions if needed and determine a coefficient of friction so that a material for the base can be chosen.
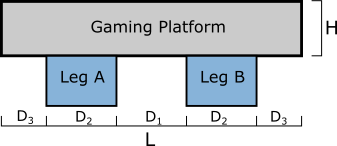
2. Sketch

3. Knows and Unknowns:
Knowns:
- FA = 10N
- D2 = 0.2m
- D3 = 0.1m
- L = 0.8m
- H = 0.15m
- m = 4kg
Unknowns:
- D1 = ?
- Fg = ?
- Ffa = ?
- Ffb = ?
- NA = ?
- NB = ?
- μ = ?
4. Approach:
Define an origin point to measure all forces from to simplify the problem.
Determine D1 and the coordinates of all forces measured from the origin O.
Find Fg.
Use sum of moment around A to find NB.
Use sum of forces in the Y direction to find NA.
Use sum of forces in the X direction to find μ.
5. Analysis:
Defining the origin as the bottom left corner of the gaming platform:
$$ N_A\ is\ measured\ D_3 + \frac{1}{2} D_2\ from\ the\ origin. \\ N_B\ is\ measured\ D_3 + D_2 + D_1 + \frac{1}{2} D_2 \ from\ the\ origin. \\ F_g\ is\ measured\ D_3 + D_2 + \frac{1}{2} D_1 \ from\ the\ origin.$$
To find D1:
$$ L = 2D_3 + 2D_2 + D_1 \\ D_1 = L – 2D_3 – 2D_2 \\ D_1 = 0.8m – 2 \cdot 0.1m – 2 \cdot 0.2m \\ D_1 = 0.2m$$
To find Fg:
$$ F_g = mg = 4kg \cdot 9.81 m/s^2 = 39.24N$$
The coordinates of these forces can now be shown as:
$$N_A\ is\ at\ [0.2, 0]m \\ N_B\ is\ at\ [0.6, 0]m \\ F_g\ is\ at\ [0.4, 0]m \\ F_A\ is\ at\ [0, 0.15]m$$
The sum of moments around point A can now be done to find NB. The distance between each force and point A is the difference of their coordinates.
$$\sum M_A = 0 = -F_g \cdot (0.4m – 0.2m) + N_B \cdot (0.6m – 0.2m) – F_A (0.15m – 0m) \\ N_B = \frac{F_g \cdot 0.2m + F_A \cdot 0.15m}{0.4m} \\ N_B = \frac{39.24N \cdot 0.2m + 10N \cdot 0.15m}{0.4m} \\ N_B = 23.37 N$$
The Sum of forces in the Y direction can be used to find NA now:
$$\sum F_y = 0 = -F_g + N_A + N_B \\ N_A = F_g – N_B = 39.24N – 23.37N \\ N_A = 15.87N$$
Before the sum of forces in the X is done, it must be noted that Ffa and Ffb are equivalent to μNA and μNB , respectively.
$$\sum F_x = 0 = F_A – F_{fa} – F_{fb} = F_A – \mu \cdot N_A – \mu \cdot N_B \\ -F_A = -\mu \cdot N_A – \mu \cdot N_B \\ \frac{-F_A}{\mu} = -N_A – N_B \\ \frac{1}{\mu} = \frac{-N_A – N_B}{-F_A} \\ \mu = \frac{-F_A}{-N_A – N_B} \\ \mu = \frac{-10N}{-15.87N – 23.37N} \\ \mu = 0.25$$
6. Review:
To review this solution, the value for NA can be solved for by taking the moment around point B.
$$ \sum M_B = 0 = F_g \cdot (0.6m – 0.4m) – N_A \cdot (0.6m – 0.2m) – F_A \cdot (0.15m) \\ N_A = \frac{(F_g \cdot 0.2m ) – (F_A \cdot 0.15m)}{0.4m} \\ N_A = \frac{(39.24N \cdot 0.2m) – (10N \cdot 0.15)}{0.15m}{0.4m} \\ N_A = 15.87N$$
The value found is the same value originally found, providing evidence that there was no error in the calculation.

