5.4 Zero-Force Members

This is a special case that is specially useful for method of joints and method of sections. These special types of members called zero-force members ensure the truss stays in a particular shape as a rigid body, but carries no load.

Zero-force members are members that you can tell just by inspection that they carry no load. They are important to the structure to ensure it stays in a rigid shape.

Zero-force members can be found considering the equilibrium equations. Look at joint e below. In the y direction, there is only 1 force: F_eh. So if the sum of the forces in the y direction $latex \sum F_{eh} = F_eh = 0, then F_eh = 0. Similarly, F_mk and F_cp are zero-force members (if you look at joint m and c). Note that if you looked at joint k or p, you couldn’t tell that F_mk and F_cp are zero-force members.

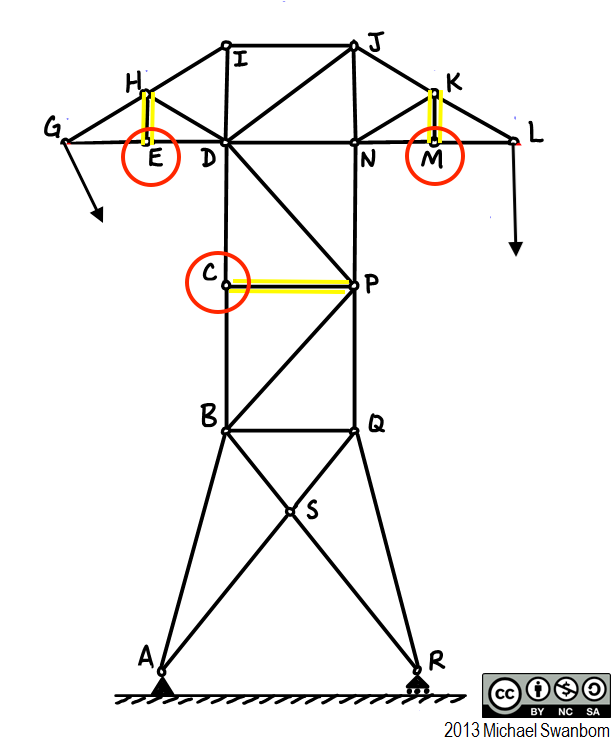
There isn’t a huge problem if you can’t find zero-force members just from inspection, but you might find that certain joints are not able to be solved as easily. (Zero-force members let you have one less unknown).

Also see that L and G have no zero-force members because the externally applied loads balance the members.

Here are some examples to practice on:

Example 1

(I count 3 zero-force members, assuming there are no loads on the bridge at the joints).

Example 2

(I count 1 zero-force member, assuming there are no loads on the bridge at the joints).

Example 3

(Looking at only 1 side of the bridge, in theory there are 7 zero-force members, but because there is a load on the deck it is more likely that all of them would be carrying a load).

Admittedly, zero-force members are more theoretical than actual.