Chapter 1: Fundamental Concepts
1.3 Vectors
1.3.1 Vector Components
Some fun facts about vectors:
- The vector is denoted with a line on top or bottom: [latex]\vec A[/latex] or A.
- There are two parts of a vector ([latex]\vec A[/latex]): magnitude (A or |A|) and direction ([latex]\underline{\hat{a}}[/latex]): [latex]\vec A = |\underline{A}|*\underline{\hat{a}}[/latex]
- In 2-dimensions, there are two components: x and y. In 3-d, there are three components: x, y, and z.
- Vectors can be denoted using Cartesian form or brackets: [latex]\vec A=A_x\underline{\hat{i}}+A_y\underline{\hat{j}}+A_z\underline{\hat{k}}[/latex] or using the bracket form horizontally: [latex]\vec A=[ A_x, A_y, A_z[/latex] ] or vertically: [latex]\vec A=\begin{bmatrix}A_x\\A_y,\\A_z \end{bmatrix}[/latex]
- The magnitude (A or |A|) is calculated using the Pythagorean theorem for each component in 2d: [latex]A = \sqrt{{A}_{x}^{2}+{A}_{y}^{2}}[/latex] and 3d: [latex]A = \sqrt{{A}_{x}^{2}+{A}_{y}^{2}+{A}_{z}^{2}}[/latex]
- The unit vector ([latex]\underline{\hat{u}}[/latex]) represents the direction in cartesian form [latex]\underline{\hat{u}}=\underline{\hat{i}}+\underline{\hat{j}}+\underline{\hat{k}}[/latex] or using bracket form: [ [latex]\underline{\hat{i}}, \underline{\hat{j}}, \underline{\hat{k}}[/latex] ].
- The magnitude of the unit vector is 1 (denoted by the ‘hat’ on top) and it is unit-less: [latex]|\underline{\hat{u}} |= \sqrt{{\underline{\hat{i}}}^{2}+{\underline{\hat{j}}}^{2}+{\underline{\hat{k}}}^{2}} = 1[/latex]
- The unit vector can be calculated from the magnitude and vector: [latex]\underline{\hat{a}} =\vec A/|A|[/latex]
In 2d & 3d:
Source: University Physics Volume 1, OpenStax CNX, https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/2-2-coordinate-systems-and-components-of-a-vector/
1.3.2 Componentizing a Vector
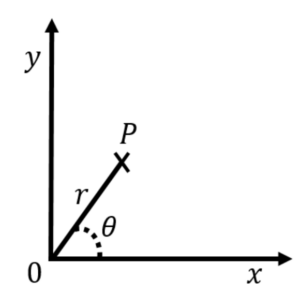
In 2d:
To find the components of a vector (A) in 2 dimensions (the x and y portions Ax and Ay), use SOH CAH TOA:
[latex]\vec A=A_x\underline{\hat{i}}+A_y\underline{\hat{j}}[/latex]
Ax = |A| cos(Θ)
Ay = |A| sin(Θ)
|A|2 = Ax2 + Ay2 (magnitude)
tan(Θ) = Ax / Ay (direction)
In 3d:
[latex]\vec A=A_x\underline{\hat{i}}+A_y\underline{\hat{j}}+A_z\underline{\hat{k}}[/latex]
|A|2 = Ax2 + Ay2+ Az2 (magnitude)
[latex]\begin{aligned} &\hat{a}=\frac{\vec A}{|\vec A|} \end{aligned}=\frac{{A}_{x} \underline{\hat{\imath}}+A_{y} \underline{\hat{\jmath}}+{A}_{z} \underline{\hat{k}}}{\sqrt{\left({A}_{x}\right)^{2}+\left({A}_{y}\right)^{2}+\left({A}_{z}\right)^{2}}}[/latex]
1.3.3 Position Vector
The position vector describes the position of an object or person from a predefined origin (a starting point, absolute 0, or some other point), for example the point where A in the above image is point at. A is the position vector. You can add individual position vectors to find the total position traveled (c = a + b), for example if someone walks from one point on campus to another, they would rarely walk in one straight line like c. In the image below, imagine that there is a building in the square near where a and b meet, so the person couldn’t take c but had to walk around. The total distance traveled is |a| + |b|, not |c| (because |c| ≠ |a| + |b|).
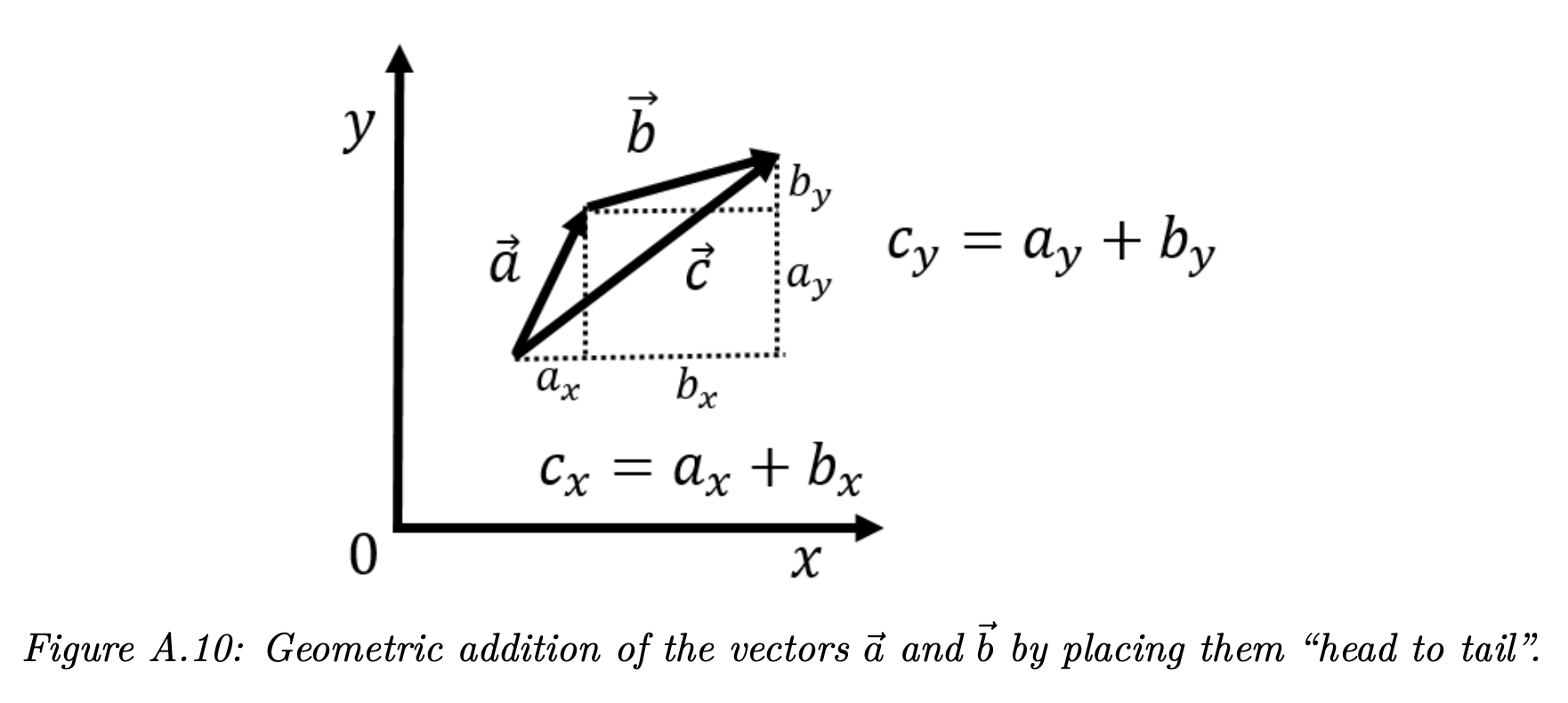
Subtraction works the same way, but instead of going from tail to head of the arrow, the reverse direction is taken, from head to tail. For example, a = c – b, follow c from tail to head, then go in the reverse direction of b from head to tail, and you end up at a.
1.3.4 Vector Math
Here’s more official language to describe vectors:
Vectors can be added together and multiplied by scalars. Vector addition is associative and commutative, and vector multiplication by a sum of scalars is distributive. Also, scalar multiplication by a sum of vectors is distributive:
[latex]\alpha(\vec A+\vec B)=\alpha\vec A +\alpha\vec B[/latex]
In this equation, α is any number (a scalar). For example, a vector antiparallel to vector [latex]\vec A=A_x\hat{i}+A_y\hat{j}+A_z\hat{k}[/latex] can be expressed simply by multiplying [latex]\vec A[/latex] by the scalar α=1:
[latex]-\vec A=-A_x\hat{i}-A_y\hat{j}-A_z\hat{k}[/latex]
The generalization of the number zero to vector algebra is called the null vector, denoted by [latex]\vec 0[/latex]. All components of the null vector are zero [latex]\vec 0 = 0 \hat{i} + 0 \hat{j} + 0 \hat{k}[/latex] , so the null vector has no length and no direction.
Two vectors [latex]\vec A[/latex] and [latex]\vec B[/latex] are equal vectors if and only if their difference is the null vector:
[latex]\vec 0=\vec A - \vec B=(A_x\underline{\hat{i}}) + A_y\underline{\hat{j}} + A_z\underline{\hat{k}}) - (B_x\underline{\hat{i}} + B_y\underline{\hat{j}} + B_z\underline{\hat{k}})[/latex]
[latex]\space=(A_x - B_x)\underline{\hat{i}} + (A_y - B_y)\underline{\hat{j}} + (A_z - B_z)\underline{\hat{k}}[/latex]
This vector equation means we must have simultaneously [latex]A_x-B_x=0[/latex], [latex]A_y-B_y=0[/latex], and [latex]A_z-B_z=0[/latex]. Hence, we can write [latex]\vec A=\vec B[/latex] if and only if the corresponding components of vectors [latex]\vec A[/latex] and [latex]\vec B[/latex] are equal:
[latex]\vec A =\vec B[/latex] if [latex]\begin{bmatrix}A_x=B_x\\A_y=B_y\\A_z=B_z\end{bmatrix}[/latex]
Two vectors are equal when their corresponding scalar components are equal.
Resolving vectors into their scalar components (i.e., finding their scalar components) and expressing them analytically in vector component form allows us to use vector algebra to find sums or differences of many vectors analytically (i.e., using graphical methods). For example, to find the resultant of two vectors [latex]\vec A[/latex] and [latex]\vec B[/latex], we simply add them component by component, as follows:
[latex]\vec R=\vec A + \vec B=(A_x\underline{\hat{i}}+A_y\underline{\hat{j}}+A_z\underline{\hat{k}})+(B_x\underline{\hat{i}}+B_y\underline{\hat{j}}+B_z\underline{\hat{k}})=(A_x+B_x)\underline{\hat{i}}+(A_y+B_y)\underline{\hat{j}}+(A_z+B_z)\underline{\hat{k}}[/latex]
In this way, scalar components of the resultant vector: [latex]\vec R=(R_x\underline{\hat{i}}+R_y\underline{\hat{j}}+R_z\underline{\hat{k}})[/latex].
[latex]\begin{matrix}R_x = A_x+B_x\\R_y = A_y+B_y\\R_z = A_z+B_z\end{matrix}[/latex]
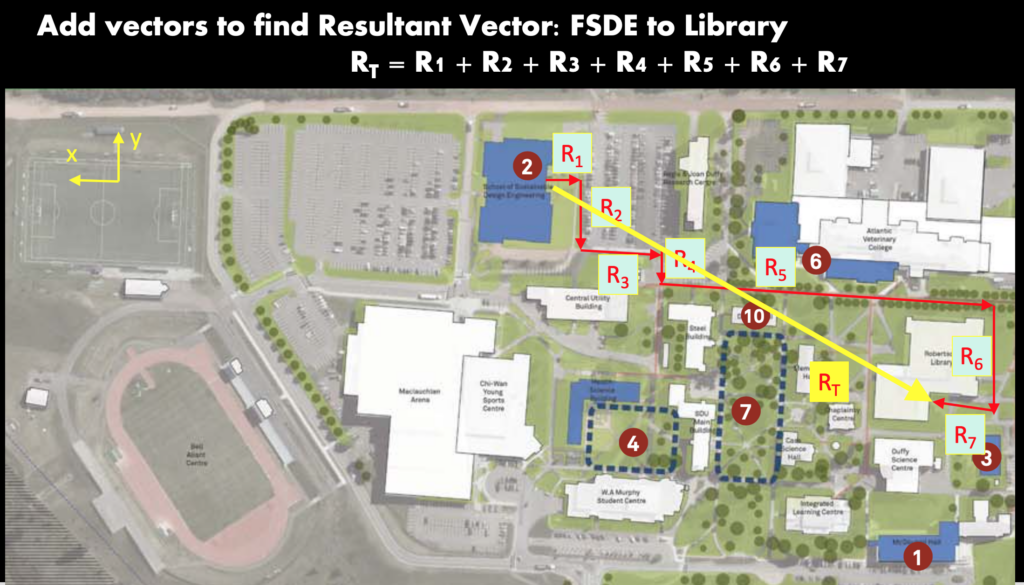
Key Takeaways
Basically: Vectors help describe position, forces, and quantities. Vectors use components, magnitude, and direction (unit vector) to do so.
Application: A hammock hangs at an angle from the wall. When a person is in the hammock, they are pulling on the wall with a force at an angle. This force vector could be componentized into x and y, using the angle and the weight of the person to calculate it.
Looking ahead: The next place vectors will appear is in Moments in 1.6.
