Chapter 2: Particles
2.2 Free Body Diagrams for Particles
A free-body diagram (FBD) helps you to simplify a complicated problem. The first thing to remember is the object should always be free which means, floating in space. You represent the floor or other surfaces with forces. You might have done these particle free body diagrams in your high school physics class, where all the forces act at the centre of the object. (This will be different for rigid bodies).
To draw a free-body diagram remember four points:
- Add coordinate frame (which way is positive x and positive y?)
- Replace surfaces with forces (floor, hand, and objects touching it become arrows)
- Point forces in the correct direction (the head of the arrow points to where the force acts. FG acts down)
- Use unique (different) names (be sure to name each force with a different name).
For a baseball being hit by a bat (and neglecting air), the force of gravity acts at the center, the force of the bat acts on the outside. Notice in the figure[1] the names FBat and FG are different in the figure below. Also – you can understand what they represent quickly. Also see the coordinate frame? You’ll be adding these in your sleep by the end of this class.
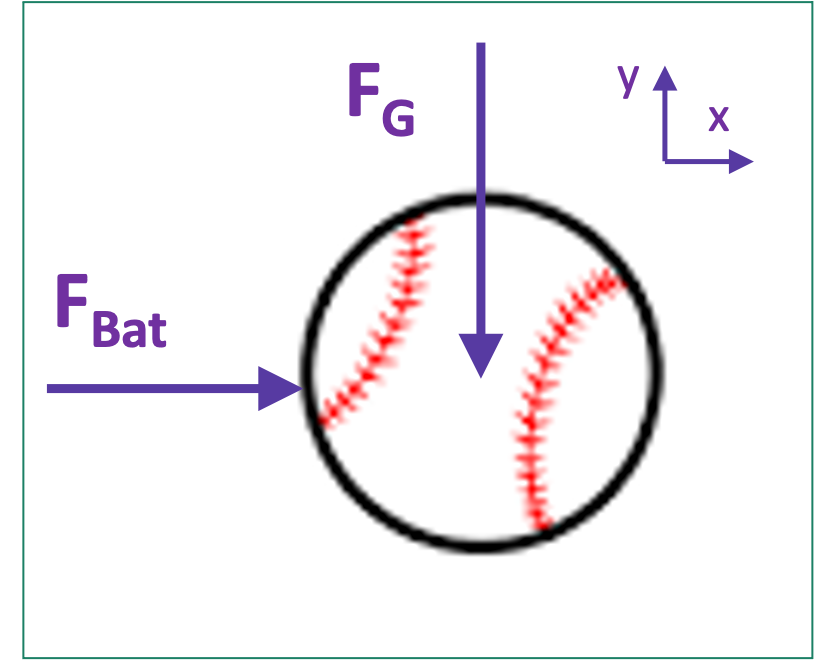
As you draw a free body diagram, there are a couple of things you need to keep in mind:
(1) Include only those forces acting ON the object whose free body diagram you are drawing. Any force exerted BY the object on some other object belongs on the free body diagram of the other object.
(2) All forces are contact forces and every force has an agent. The agent is “that which is exerting the force.” In other words, the agent is the life form or thing that is doing the pushing or pulling on the object. No agent can exert a force on an object without being in contact with the object.
We are going to introduce the various kinds of forces by means of examples. Here is the first
example:
A rock is thrown up into the air by a person. Draw the free body diagram of the rock while it is up in the air. (Your free body diagram is applicable for any time after the rock leaves the thrower’s hand, until the last instant before the rock makes contact with whatever it is destined to hit.) Neglect any forces that might be exerted on the rock by the air.
If you see the rock flying through the air, it may very well look to you like there is nothing touching the rock. But the earth’s gravitational field is everywhere in the vicinity of the earth. It can’t be blocked. It can’t be shielded. It is in the air, in the water, even in the dirt. It is in direct contact with everything in the vicinity of the earth. It exerts a force on every object near the surface of the earth. We call that force the gravitational force. You have already studied the gravitational force. We give a brief synopsis of it here.
The Gravitational Force Exerted on Objects Near the Surface of the Earth.
Because it has mass, the earth has a gravitational field. The gravitational field is a force-per-mass field. It is invisible. It is not matter. It is an infinite set of force-per-mass vectors, one at every point in space in the vicinity of the surface of the earth. Each force per-mass vector is directed downward, toward the center of the earth and, near the surface of the earth, has a magnitude of 9.81 N/kg. The effect of the earth’s gravitational field is to exert a force on any object that is in the earth’s gravitational field. The force is called the gravitational force and is equal to the product of the mass of the object and the earth’s gravitational field vector: Fg=mg. Where g=9.81 N/kg is the magnitude of the earth’s gravitational field vector. The direction of the near-earth’s-surface gravitational force is downward, toward the center of the earth.
Here is the free body diagram and the corresponding table of forces:
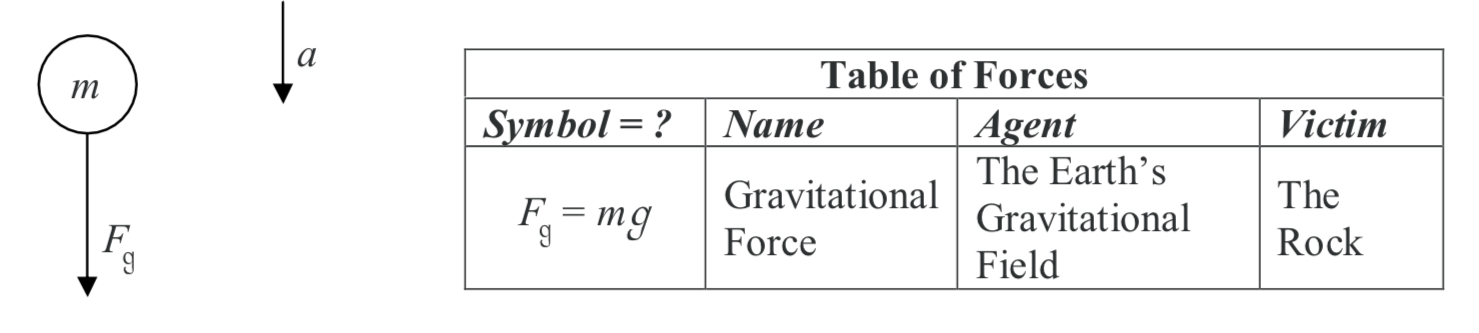
(1) The only thing touching the object while it is up in the air (neglecting the air itself) is the earth’s gravitational field. So there is only one force on the object, namely the gravitational force. The arrow representing the force vector is drawn so that the tail of the arrow is touching the object, and the arrow extends away from the object in the direction of the force.
(2) Unless otherwise stipulated, label the diagram yourself however it makes most sense. Always draw a coordinate frame (Usually x is upwards, and y extends to the right).
(3) There is no velocity information on a free body diagram
(4) There is no force of the hand acting on the object because, at the instant in question, the hand is no longer touching the object. When you draw a free body diagram, only forces that are acting on the object at the instant depicted in the diagram are included. The acceleration of the object depends only on the currently-acting forces on the object. The force of the hand is of historical interest only.
(5) Regarding the table of forces:
a) Make sure that for any free body diagram you draw, you are capable of making a complete table of forces. You are not required to provide a table of forces with every free body diagram you draw, but you should expect to be called upon to create a table of forces more than once.
b) In the table of forces, the agent is the life form or thing that is exerting the force and the victim is the object on which the force is being exerted. Make sure that, in every case,
the victim is the object for which the free body diagram is being drawn.
c) In the case at hand, there is only one force so there is only one entry in the table of forces.
d) For any object near the surface of the earth, the agent of the gravitational force is the earth’s gravitational field. It is okay to abbreviate that to “Earth” because the gravitational field of the earth can be considered to be an invisible part of the earth, but it is NOT okay to call it “gravity.” Gravity is a subject heading corresponding to the kind of force the gravitational force is, gravity is not an agent
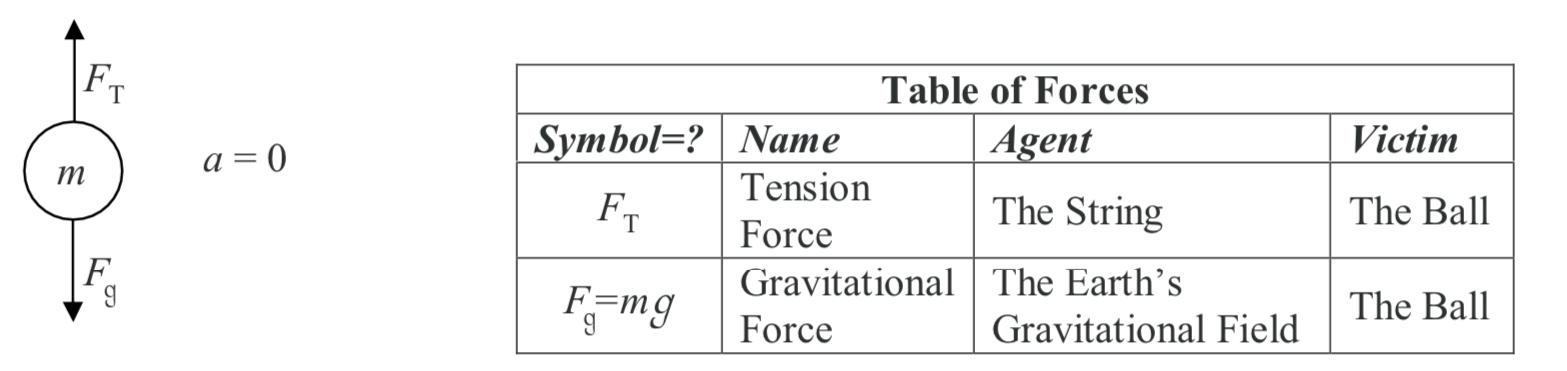
A ball of mass m hangs at rest, suspended by a string. Draw the free body diagram for the ball, and create the corresponding table of forces.
To do this problem, you need the following information about strings:
The Force Exerted by a Taut String on an Object to Which it is Affixed (This also applies to ropes, cables, chains, and the like.)
The force exerted by a string, on an object to which it is attached, is always directed away from the object, along the length of the string. Note that the force in question is exerted by the string, not for instance, by some person pulling on the other end of the string. The force exerted by a string on an object is referred to as a “tension force” and its magnitude is conventionally represented by the symbol FT.
Note: There is no formula to tell you what the tension force is. If it is not given, the only way to get it is to use Newton’s 2nd Law.
Here is the free body diagram of the ball, and the corresponding table of forces:
There is no “force of motion” acting on an object. Once you have the force or forces
exerted on the object by everything that is touching the object, you have all the forces. Do not add a “force of motion” to your free body diagram. It is especially tempting to add this force when there are no actual forces in the direction in which an object is going. Keep in mind, however, that an object does not need a force on it to keep going in the direction in which it is going; moving along at a constant velocity is what an object does when there is no net force on it.
Source: Calculus-Based Physics 1, Jeffery W. Schnick. https://openlibrary.ecampusontario.ca/catalogue/item/?id=ce74a181-ccde-491c-848d-05489ed182e7 page 86
Key Takeaways
Basically: Free-body diagrams (FBDs) give you a way to model complicated problem in a simple way. All exterior forces are modeled with an arrow.
Application: A baseball can be modeled using a FBD to show how the bat and gravity affect the ball.
Looking ahead: You’ll use a FBD in every step 2 in nearly every homework problem. These are especially helpful with Equilibrium Equations in the next section.
- Original image of baseball from: https://openclipart.org/detail/258473/baseball-refixed Annotations added by the author ↵

