Chapter 7: Inertia
7.6 Examples
Here are examples from Chapter 7 to help you understand these concepts better. These were taken from the real world and supplied by FSDE students in Summer 2021. If you’d like to submit your own examples, please send them to the author eosgood@upei.ca.
Example 7.6.1: All of Ch 7 – Submitted by William Craine
1. Problem
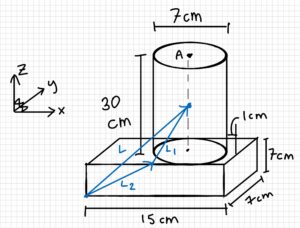
A person is playing soccer. The ball they are using has a diameter of 20 cm, and a mass of 0.45 kg. The person’s leg has a mass of 18 kg, and their foot has a mass of 8 kg. Assume that all the shapes are uniform density.
a) Find the cm for the ball.
b) Calculate the mass moment of inertia (MMOI) for the ball.
c) Find the cm for the person’s leg and foot.
d) Find the MMOI for the person’s leg and foot on the y-axis about A.

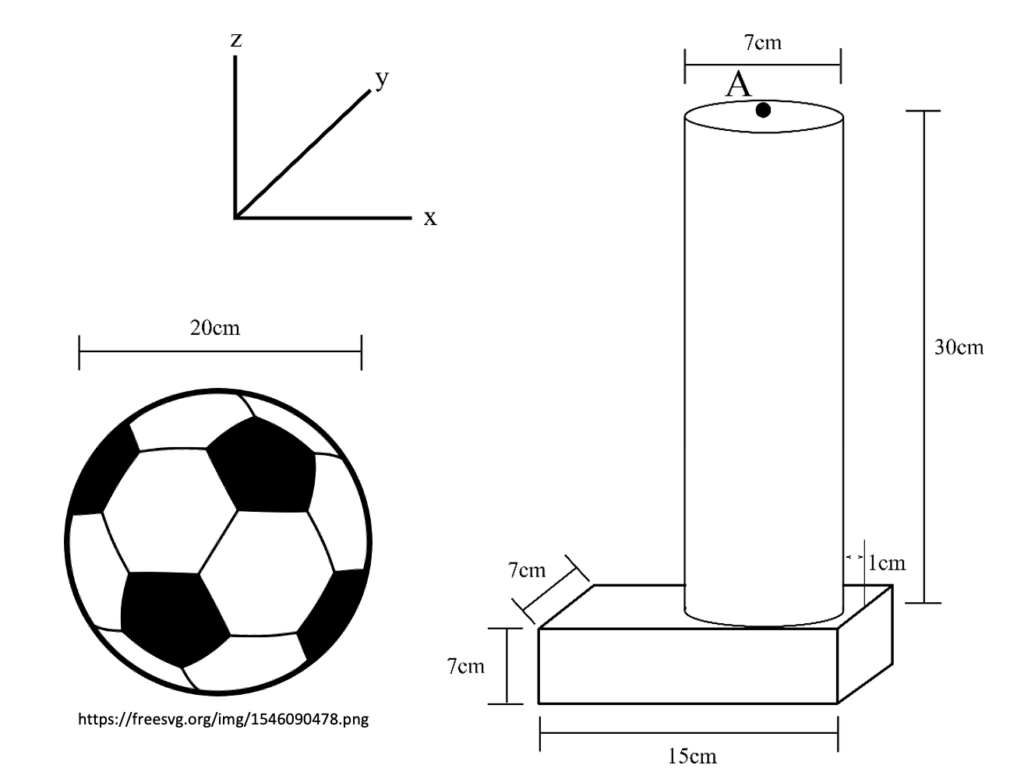
2. Draw
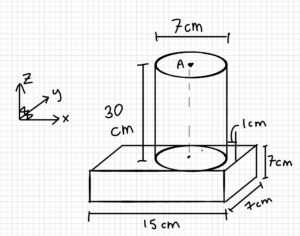
3. Knowns and Unknowns
Knowns:
- mb = 0.45 kg
- db = 20 cm
- mL = 18 kg
- mf = 8 kg
Unknowns:
- xb
- Ib
- xp
- Ip x
4. Approach
Find the cm for both objects using arbitrary coordinates since no origin is given.
Use the sphere MMOI formula for the ball.
Calculate the individual MMOIs for the leg and foot, then use parallel axis theorem to get each shape’s MMOI about the system cm, add them, and then use parallel axis theorem to get MMOI about A.
5. Analysis
Part a (find the center of mass of the ball):
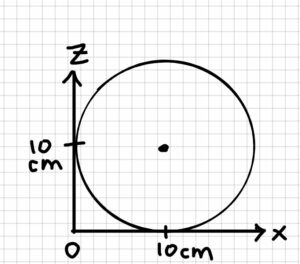
$$x_b=(10\underline{\hat{i}}+10\underline{\hat{j}}+10\underline{\hat{k}})cm$$
Part b (find the MMOI of the ball about its center of mass):
$$I_{xx}=I_{yy}=I_{zz}=\frac{2}{3}mr^2\\\qquad \quad=\frac{2}{3}(0.45 kg)(0.1m)^2\\I_b=0.003kgm^2$$
Part c (find the center of mass for the system of the person’s leg):
Step 1: find the center of mass of the foot (f)
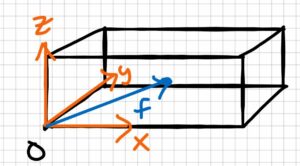
$$f=\frac{15cm}{2}\underline{\hat{i}}+\frac{7cm}{2}\underline{\hat{j}}+\frac{7cm}{2}\underline{\hat{k}}\\f=(7.5\underline{\hat{i}}+3.5\underline{\hat{j}}+3.5\underline{\hat{k}})cm$$
Step 2: find the center of mass of the leg (L)
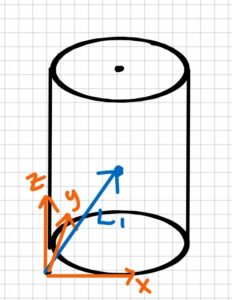
$$L_1=(3.5\underline{\hat{i}}+3.5\underline{\hat{j}}+15\underline{\hat{k}})cm\\L_2=(15cm-7cm-1cm)\underline{\hat{i}}+(0cm)\underline{\hat{j}}+(7cm)\underline{\hat{k}}\\\qquad \quad L_2 = (7 \underline{\hat{i}}+(0)\underline{\hat{j}}+(7)\underline{\hat{k}} )cm$$
$$\\L=L_1+L_2\\L=(3.5cm+7cm)\underline{\hat{i}}+(3.5cm+0cm)\underline{\hat{j}}+(15cm+7cm)\underline{\hat{k}}\\L=(10.5\underline{\hat{i}}+3.5\underline{\hat{j}}+22\underline{\hat{k}})cm$$
Step 3: find the center of mass of the system (P)
$$x_p=\frac{\sum m_i x_i}{\sum m_i}\\X_p=\frac{m_f\cdot x_f+m_L\cdot x_L}{m_f+m_L}\\x_p=\frac{8kg\cdot 7.5cm+18kg\cdot 10.5cm}{8kg+18kg}\\x_p=9.58cm$$
$$y_p=\frac{\sum m_i y_i}{\sum m_i}\\y_p=\frac{8kg\cdot 3.5cm+18kg\cdot 3.5cm}{8kg+18kg}\\y_p=3.5cm$$
$$z_p=\frac{\sum m_i z_i}{\sum m_i}\\z_p=\frac{8kg\cdot 3.5cm+18kg\cdot 22cm}{8kg+18kg}\\z_p=16.3cm$$
$$\underline{\underline{P}=(9.58\underline{\hat{i}}+3.5\underline{\hat{j}}+16.3\underline{\hat{k}})cm}$$
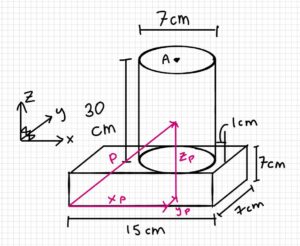
Part d (find the inertia of the person’s leg about point A):
Step 1: Find the MMOI of the foot about f (Iff)
$$x_f=0.15m\\z_f=0.07m\\m_f=8kg$$
$$I_{ff}=\frac{1}{12}\cdot m\cdot (x^2+z^2)\\I_{ff}=\frac{1}{12}(8kg)(0.15m^2+0.07m^2)\\I_{ff}=0.0182kg\; m^2$$
Step 2: Find the MMOI of the foot about P (IPf)
$$ d^2=(0.0208m)^2+(0.128m)^2\\I_{pf}=I_{ff}+m_f(d_f)^2\\I_{pf}=0.0182kgm^2+8kg[(0.0208m)^2+(0.128m)^2]\\I_{pf}=0.1527kgm^2$$
Step 3: Find the MMOI of the leg about L (ILL)
$$r=0.035m\\h=0.3m\\m_L=18kg\\I_{LL}=\frac{1}{12}\cdot m\cdot (3_r^2+h^2)\\I_{LL}=\frac{1}{12}\cdot 18kg(3(0.035m)^2+(0.3m)^2)\\I_{LL}=0.1405kgm^2$$
Step 4: Find the MMOI of the leg about P (IPL)
$$r_{LP}=[(9.58-10.5)\underline{\hat{i}}+(3.5-3.5)\underline{\hat{j}}+(16.3-22)\underline{\hat{k}}]cm\\r_{LP}=(-0.92\underline{\hat{i}}-5.7\underline{\hat{k}})cm\\I_{PL}=I_{LL}+m(d^2)\\I_{PL}=0.1405kgm^2+18kg[(0.0092m)^2+(0.057m)^2]\\I_{PL}=0.2005kgm^2$$
Step 5: Find the MMOI of the entire system about P (IP)
$$I_p=I_{PL}+I_{pf}\\I_p=0.1527kgm^2+0.2005kg\\I_p=0.3532kgm^2$$
Step 6: Find the MMOI of the entire system about A (IA)
$$A=(10.5\underline{\hat{i}}+3.5\underline{\hat{j}}+37\underline{\hat{k}})cm\\P=(9.58\underline{\hat{i}}+3.5\underline{\hat{j}}+16.3\underline{\hat{k}})cm\\r_{AP}=P-A\\r_{AP}=[(9.58-10.5)\underline{\hat{i}}+(3.5-3.5)\underline{\hat{j}}+(16.3-37)\underline{\hat{k}}]cm\\r_{AP}=(-0.92\underline{\hat{i}}-20.7\underline{\hat{k}})cm$$
$$I_A=I_p+m(d^2)\\I_A=0.3532kgm^2+(8kg+18kg)[(0.0092m)^2+(0.207m)^2]\\I_A=1.4695kgm^2\\\underline{I_A=1.47kgm^2}$$
6. Review
It makes sense that the numbers are small, since before the final step, the mass was small, or the distance to the new axis was small.
Example 7.6.2 Inertia – Submitted by Luke McCarvill
1. Problem
A figure skater with a mass of 60 kg is about to perform a spin about her long axis (z). She is 167 cm tall, and her body can be approximated as a circular cylinder of 30 cm diameter while her limbs are at her side, and a circular cylinder of 60 cm diameter while her arms (and one leg) are outstretched.
a) What should she do in order to generate the highest angular acceleration, assuming she can generate a net torque of 200 Nm? Does lowering her height increase or decrease her angular acceleration?
b) How fast will she be spinning after 0.5 seconds of her maximum vs minimum accelerations, assuming she starts from zero (⍵0 = 0 rad/sec)?
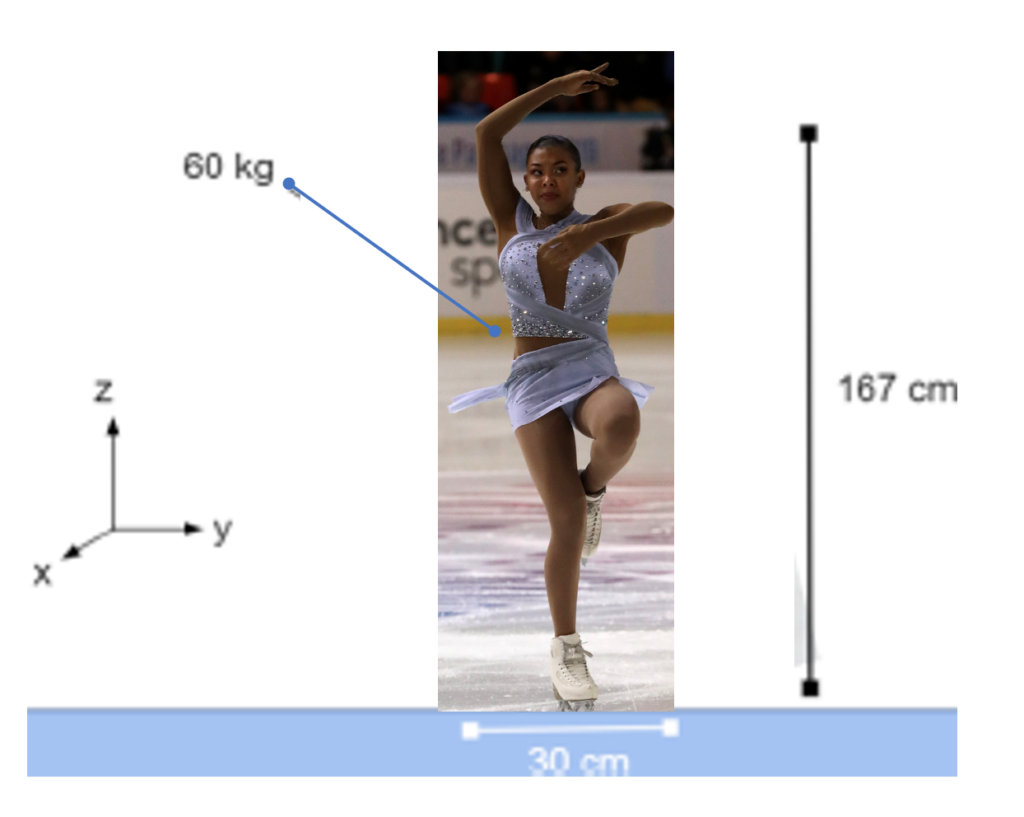
2. Draw
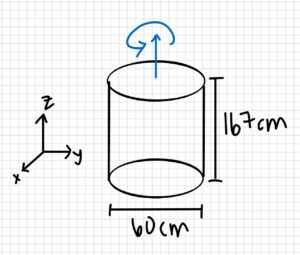
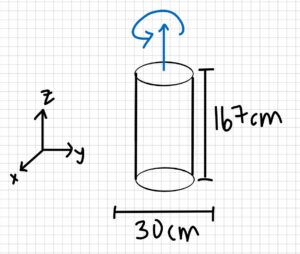
3. Knowns and Unknowns
Knowns:
- m = 60 kg
- ΣM = 200Nm
- h = 167cm
- d1 = 30cm
- d2 = 60cm
- t = 0.5sec
- Izz = ½ mr2
- ΣM = I∝
- ⍵0 = 0rad/sec
Unknowns:
- ∝1 = ?
- ∝2 = ?
- Izz1 = ?
- Izz2 = ?
- ⍵1 = ?
- ⍵2 = ?
4. Approach
I’ll be using MMOI for circular cylinders, as well as the sum of moments/torque equaling MMOI times angular acceleration, as well as acceleration equaling change in velocity over time.
5. Analysis
Part a:
Step 1: find the inertia when the arms are hugged to the body
Izz1 = 0.5 (60kg) (0.15m)2
Izz1= 0.675 kg m2
Step 2: find the inertia when the arms are spread out
Izz2 = 0.5(60kg)(0.3m)2
Izz2 = 2.7 kg m2
Step 3: find the angular acceleration for both cases
ΣM = I∝ therefore ΣM/I = ∝
∝1 = ΣM / Izz1
∝1 = 200 Nm / 0.675 kg m2
∝1 ≈ 296.296 rad/sec2
∝2 = ΣM / Izz2
∝2 = 200Nm/2.7 kg m2
∝2 ≈ 74.074 rad/sec2
The acceleration when the skater had her arms close to her body was about 296 rad/sec2, while that when she had her arms spread out was about 74 rad/sec2. Therefore, having her limbs closer to her body will give her a much higher angular acceleration!
As seen in the equation Izz = ½ m r2, her height is arbitrary, thus lowering her height would not change the inertia nor will it change her angular acceleration.
Part b:
∝ = ⍵/t therefore ∝*t = ⍵
⍵1 = 296.296 s-2(0.5s)
⍵1 = 148.148 rad/sec
⍵2 = 74.074 s-2(0.5s)
⍵2 = 37.037 rad/sec
Given that these are in radians per second, let’s convert this to rotations per second to make it more meaningful. To do so, simply divide by 2pi since there are 2pi radians per rotation. Thus, with her arms in, she can achieve about 23.6 rotations per second after 0.5 seconds of acceleration, compared to about 5.9 rotations per second with her limbs out. This is on par with an Olympian according to this site.
6. Review
It makes sense that they spin faster when their limbs are hugged to their body; we can try this at home with a swivel chair!

