Chapter 7: Inertia
7.5 Inertia Intro: Parallel Axis Theorem
There are two great uses for the parallel axis theorem:
1. Finding the inertia of a complex object with multiple parts.
2. Rotating an object about an axis other than through the center of mass (y’)
To begin with, the parallel axis theorem is equal to the inertia about the center of mass (Icm) plus the distance between the axes of rotation squared times the mass.
$$I=I_{cm}+md^2$$
Example 1:
For a disk, the distance between axes y and y’ is d and the [latex]I_{cm} = \frac{1}{2}mr^2[/latex].
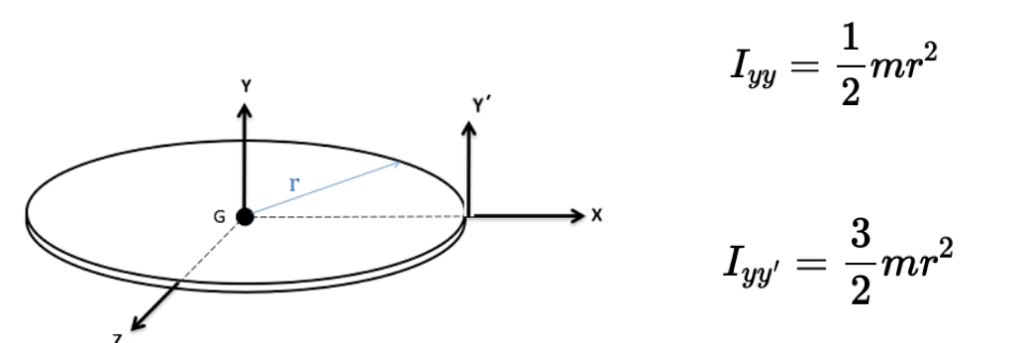
$$I=I_{cm}+md^2 = \frac{1}{2}mr^2+mr^2 = \frac{3}{2}mr^2$$
You will need the table of common geometric shapes in the previous section to find the Icm for each object.
- I is the moment of inertia of an object with respect to an axis from which the center of
mass of the object is a distance d. - ICM is the moment of inertia of the object with respect to an axis that is parallel to the first axis and passes through the center of mass.
- m is the mass of the object.
- d is the distance between the two axes.
The parallel axis theorem relates the moment of inertia ICM of an object, with respect to an axis through the center of mass of the object, to the moment of inertia I of the same object, with respect to an axis that is parallel to the axis through the center of mass and is at a distance d from the axis through the center of mass.
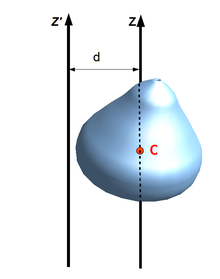
A conceptual statement made by the parallel axis theorem is one that you probably could have arrived at by means of common sense, namely that the moment of inertia of an object with respect to an axis through the center of mass is smaller than the moment of inertia about any axis parallel to that one. As you know, the closer the mass is “packed” to the axis of rotation, the smaller the moment of inertia; and; for a given object, per definition of the center of mass, the mass is packed most closely to the axis of rotation when the axis of rotation passes through the center of mass. The PAT is visually shown below, as z represents the axis on which the objects COM rotates about, z’ is the axis it is now going to rotate about, and d is the distance between these two axis’.
Source: Calculus-Based Physics 1, Jeffery W. Schnick. https://openlibrary.ecampusontario.ca/catalogue/item/?id=ce74a181-ccde-491c-848d-05489ed182e7
Steps for finding the MMOI of an object
- Determine the shape of the object (or shapes, if it a composite object).
- Determine which axis the object is rotating about.
- Find the center of mass for each individual shape.
- Find the ICM (inertia about its center of mass) for each shape.
- Determine the distance from the CM of the shapes to the axis of rotation.
- Use the Parallel Axis Theorem to find the inertia for each shape.
- Add up all these individuals inertias to find IT.
Example 2:
Find the moment of inertia of a uniform rod with ICM=0.05kgm2, L=0.08m, and mass=0.250kg, with respect to an axis that is perpendicular to the rod and passes through at 1/4 of the length of the rod.
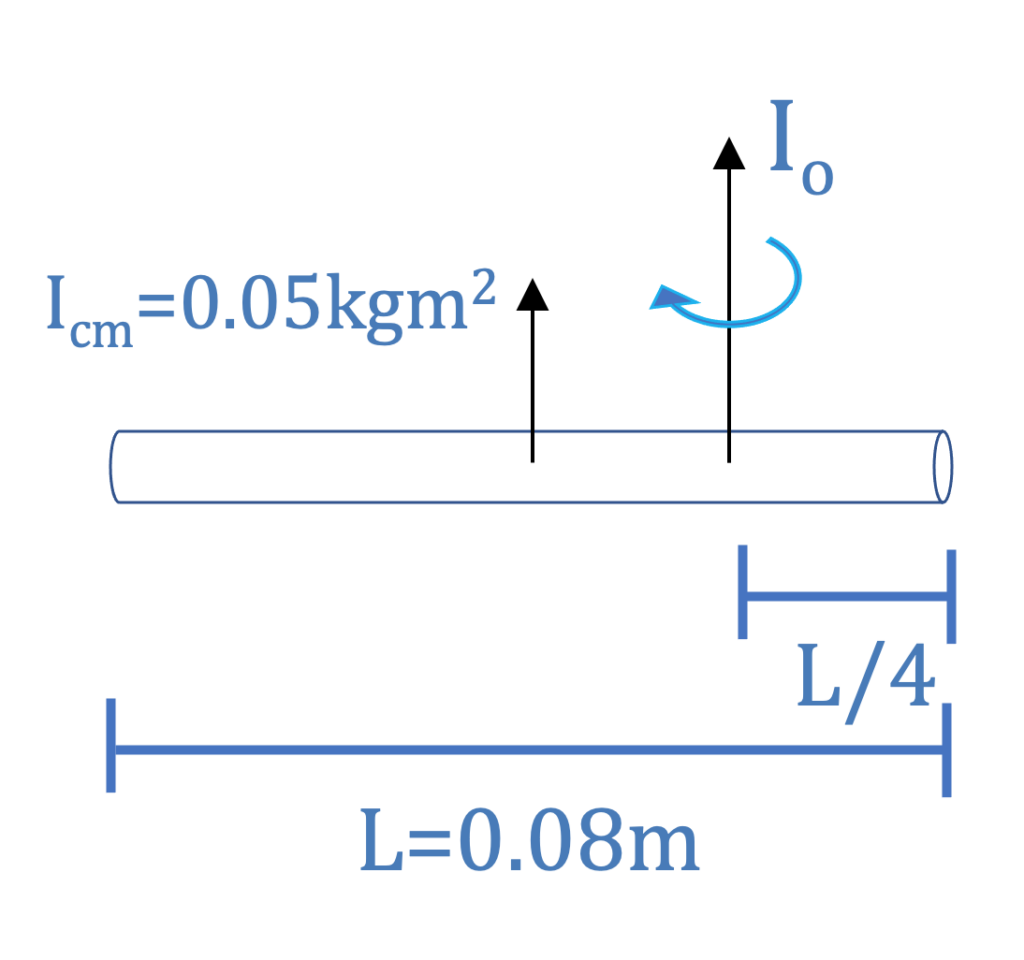
We know the distance (d) to be L/4 = 0.08m / 4 = 0.02m away from the z axis. Here we present the solution to the problem:
I=ICM + md2
I=0.05 kgm2 + (0.250kg)(0.02m)2
I=0.0501 kgm2
Example 3
A dumbbell consists of two .2 meter diameter spheres, each with a mass of 40 kg, attached to the ends of a .6 meter long, 20 kg slender rod. Determine the mass moment of inertia of the dumbbell about the y axis shown in the diagram.
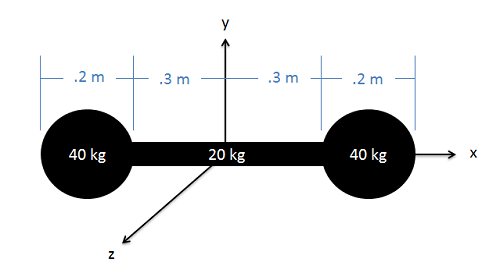
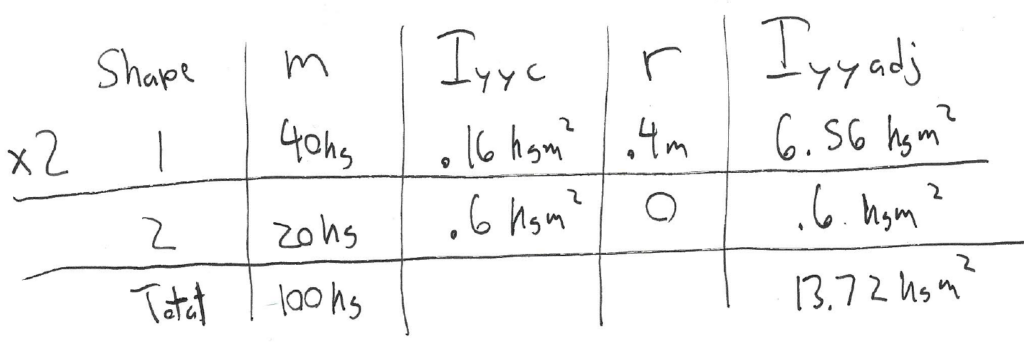
Organize the known and unknown data in a table to complete as you go:
Find the center of mass:
- For each sphere, the rcm is 0.3m + 1/2 radius = 0.3m + 1/2 (0.2m) = 0.4m
- For the bar, the rcm is at 0.
Find the inertia about the center of mass for each shape separately. Use the rectangle equation:
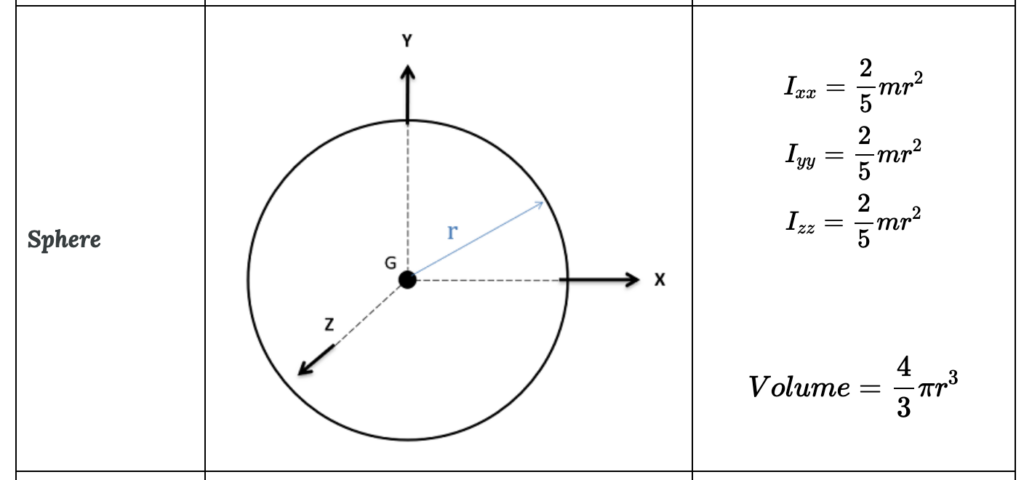
For the sphere:
$$ I_{cm-sph}=\frac{2}{5}mr^2 =\frac{2}{5}*(40kg)*(0.1m)^2 \\ \qquad \quad =0.16kgm^2$$
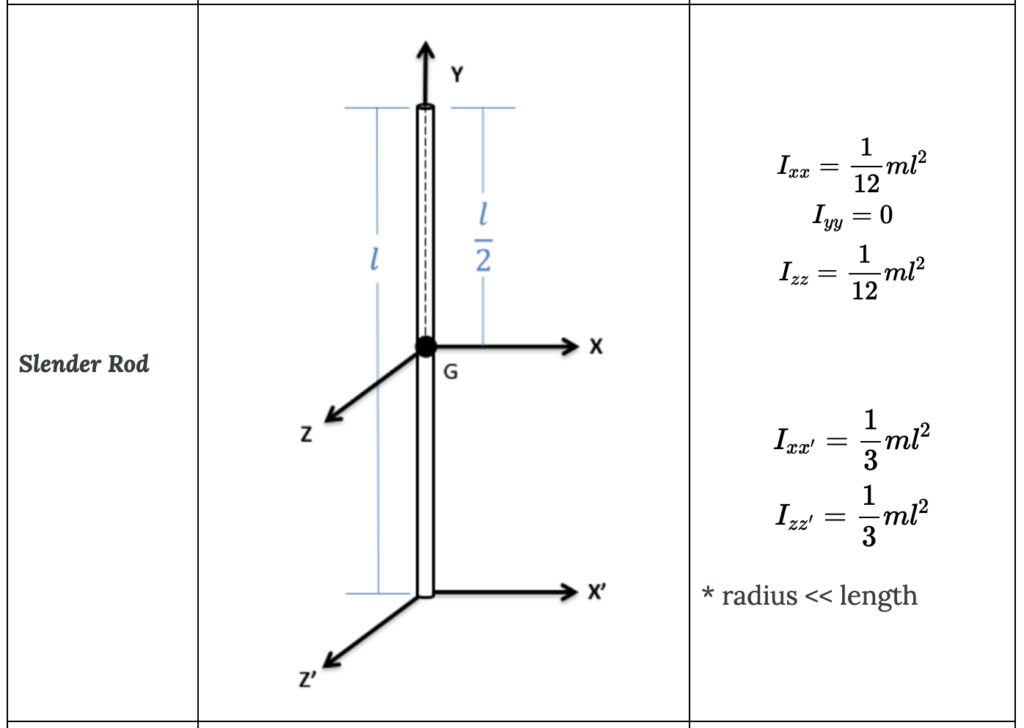
For the rod,
$$I_{cm-rod}=\frac{1}{12}ml^2 = \frac{1}{12}*(20kg)*(0.6m)^2\\\qquad \quad = 0.6 kgm^2$$
Next the parallel axis theorum is needed to change the axis of rotation from the cm of the sphere to the system cm. The distance between axes of rotation is 0.3m + 1/2 radius = 0.3m + 1/2 (0.2m) = 0.4m
$$I_{o-sph}=I_{cm-sph}+md^2 = 0.16 kgm^2 + (40kg)*(0.4m)^2 \\\qquad \quad = 6.56kgm^2$$
Finally, add up the parts: the 2 spheres and the cm of the rod:
$$I_{total} = 2 * I_{o-sph}+I_{cm-rod}\\\qquad \quad = 2*(6.56 kgm^2) + (0.6 kgm^2)\\\qquad \underline{I_{total} = 13.72 kgm^2}$$
Source: mechanicsmap.psu.edu/websites/A2_moment_intergrals/parallel_axis_theorem/parallelaxistheorem.html
Key Takeaways
Basically: The parallel axis theorem helps you to find the inertia about a different axis of rotation than the cg, and it lets you combine multiple objects.
Application: Find the total inertia of shape with multiple objects.
Looking Ahead: This will be used throughout dynamics.

