Chapter 3: Rigid Body Basics
3.5 Indeterminate Loads
Determinate Loads
Once you have your equilibrium equations, you can solve them for unknowns using algebra. The number of unknowns that you will be able to solve for will be the number of equilibrium equations that you have. In the x-y-z coordinate frame, there are 3 equations. so there can be 3 unknowns. These are statically determinate.
Typically, reaction forces are either as follows: a roller and a pinned reaction force together (1 reaction force + 2 reaction forces = 3 restraints) or a fixed beam (2 reaction forces and 1 moment = 3 restraints).
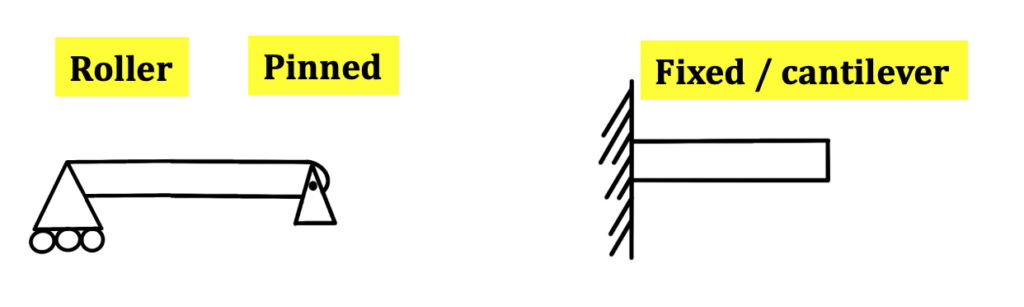
Indeterminate Loads
When you have more unknowns than equations, the problem is a statically indeterminate problem and you will need additional information to solve for the given unknowns. You’ll learn how to model and solve for these problems in your Structures course, but for Statics you need to be able to identify what is determinate and what is indeterminate.
Essentially, a problem in statically indeterminate if there are more unknown variables then there are equations you can use to solve for the unknowns. This means it cannot be solved using equilibrium equations alone. You would need to simplify the problem or make as assumption for it to be solved. You’ll look into that more in Structures, because in real life, we want redundancy. We want to be sure that structures are strong and one part can fail but that the whole building doesn’t collapse. However, we cannot over-constrain something so that is breaks because it has no way to expand during heat or cooling. All of this makes it harder to model, but safer to use.
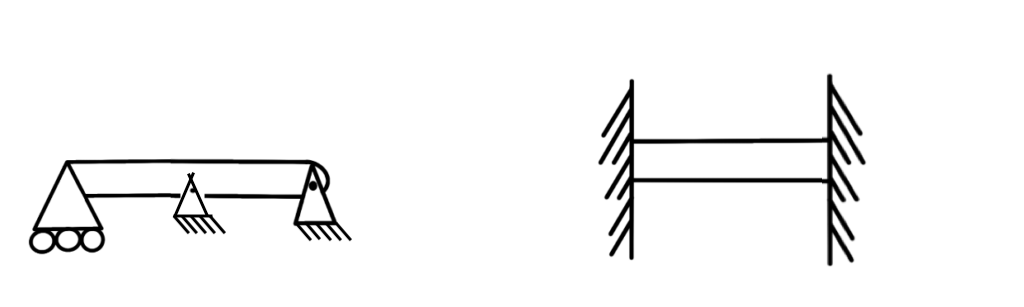
Here are examples of statically indeterminate problems:
Here is a real world example of beams. Notice the breaks between sections (in the yellow circles) to allow for expansion and contraction. The top beam in between yellow circles would be an example of a pin and roller system where one side is pinned and the other side is a roller allowing for horizontal expansion.

Examples of statically indeterminate structures:
Source: ” Equilibrium Structures, Support Reactions, Determinacy and Stability of Beams and Frames” by LibreTexts is licensed under CC BY-NC-ND . https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.03%3A_Equilibrium_Structures_Support_Reactions_Determinacy_and_Stability_of_Beams_and_Frames
Key Takeaways
Basically: When you have more unknowns than equations, the problem is a statically indeterminate problem
Application: Most situations are statically indeterminate, such as how beams are supported to provide for redundancy, thus we make assumptions to model a problem using equilibrium equations.
Looking Ahead: In Structures you will learn how to solve for statically indeterminate problems. In Statics, you need to be able to identify them.
Written by Gayla & Libby



