Chapter 2: Particles
2.3 Equilibrium Equations for Particles
For a particle in static equilibrium, Newton’s 2nd law can be adapted for [latex]\vec a = 0[/latex] and componentized in x y and z:
$$\sum\vec F=m*\vec a$$
$$\sum\vec F=0$$
$$\sum F_x=0\quad\quad\sum F_y=0\quad\quad\sum F_z=0$$
Notice that the left size of the equation says ‘sum of the forces’ which means add up all the forces in that direction. In statics, they will all cancel out. If you aren’t sure if something is in static motion, sum the forces and see if they equal 0.
Static Equilibrium:
Objects in static equilibrium are objects that are not accelerating (either linear acceleration or angular acceleration). These objects may be stationary, or they may have a constant velocity.
Newton’s Second Law states that the force exerted on an object is equal to the mass of the object times the acceleration it experiences. Therefore, if we know that the acceleration of an object is equal to zero, then we can assume that the sum of all forces acting on the object is zero. Individual forces acting on the object, represented by force vectors, may not have zero magnitude but the sum of all the force vectors will always be equal to zero for objects in equilibrium.
The equations used when dealing with particles in equilibrium are:
$$\sum\vec F=0$$
Which leads to:
$$\sum F_x=0\\\sum F_y=0\\\sum F_z=0$$
Since it is a particle, there are no moments involved like there is when it comes to rigid bodies.
Source: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/2_equilibrium_concurrent/2-1_static_equilibrium/staticequilibrium.html
Finding the Equilibrium Equations:
The first step in finding the equilibrium equations is to draw a free body diagram of the body being analyzed. This diagram should show all the known and unknown force vectors acting on the body. In the free body diagram, provide values for any of the know magnitudes or directions for the force vectors and provide variable names for any unknowns (either magnitudes or directions).
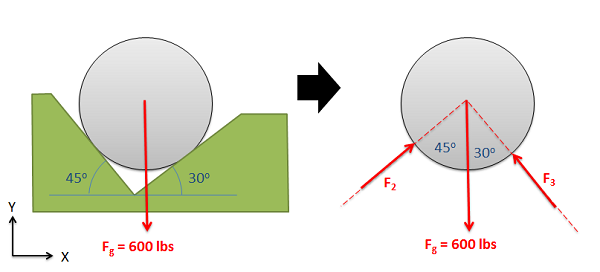
Next you will need to chose the x, y, and z axes. These axes do need to be perpendicular to one another, but they do not necessarily have to be horizontal or vertical. If you choose coordinate axes that line up with some of your force vectors you will simplify later analysis.
Once you have chosen axes, you need to break down all of the force vectors into components along the x, y and z directions (see the vectors page in Appendix 1 if you need more guidance on this). Your first equation will be the sum of the magnitudes of the components in the x direction being equal to zero, the second equation will be the sum of the magnitudes of the components in the y direction being equal to zero, and the third (if you have a 3D problem) will be the sum of the magnitudes in the z direction being equal to zero. Collectively these are known as the equilibrium equations.
Once you have your equilibrium equations, you can solve them for unknowns using algebra. The number of unknowns that you will be able to solve for will be the number of equilibrium equations that you have. In instances where you have more unknowns than equations, the problem is known as a statically indeterminate problem and you will need additional information to solve for the given unknowns.
Example:
1. Problem
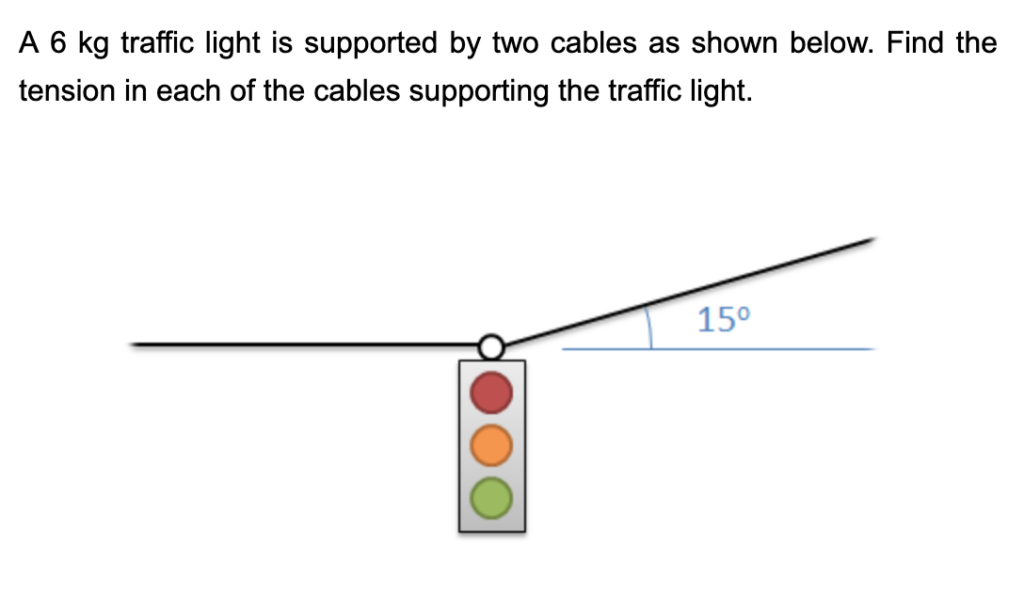
2. Draw
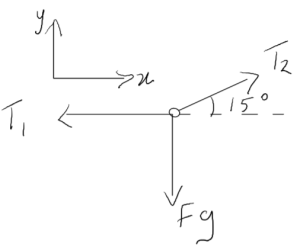
3. Knowns and Unknowns
Known:
- Mg = 6kg
Unknown:
- T1
- T2
4. Approach
Derive equilibrium equations and solve simultaneously to find T2 and T1
5. Analysis
$$F_g=(9.8)(6)\\F_g=58.8N\\\sum F_x=-T_1+T_2\cos(15^{\circ})=0\\\sum F_y=T_2\sin(15^{\circ})-58.8=0\\T_2=\frac{58.8}{\sin(15^{\circ})}=227.2N\\-T_1+227.2\cos(15^{\circ})=0\\T_1=227.2\cos(15^{\circ})=219.4N\\T_1=219.4N\\T_2=227.2N$$
6. Review
It makes sense that the tension in T2 is greater than T1 since it is at an angle.
Source: Engineering Mechanics, Jacob Moore, et al. Mechanics Map – Equilibrium Analysis for Concurrent Force Systems. Many more examples are available at this site.
Key Takeaways
Basically: Equilibrium equations allow you to separate the forces and motion into each axis.
Application: A heavy object is lifted using a rope and pulley. Based on the forces, is it in static equilibrium? (Answer: if sum of the forces in each direction equal zero, then yes!)
Looking ahead: We will next apply equilibrium equations to rigid bodies, allowing use to solve more complex problems.

