Chapter 4: Rigid Bodies
4.3 Rigid Body Equilibrium Equations
We use the equilibrium equations to calculate any unknown forces & moments using the known forces and values, and the following equations:
The particle equilibrium equations were covered in section 2.3. These are:
$$
\Sigma F_{x}=0, \Sigma F_{y}=0, \Sigma F_{z}=0
$$
Now for a rigid body where forces are analyzed at different points on a body, we can take moments into account. There are 3 equations for 2d and 4 equations for 3d:
Rigid Body-Two Dimensions
$$
\Sigma F_{x}=0, \Sigma F_{y}=0, \Sigma M_{O}=0
$$
Rigid Body-Three Dimensions
$$
\begin{gathered}
\Sigma F_{x}=0, \Sigma F_{y}=0, \Sigma F_{z}=0 \\
\Sigma M_{x^{\prime}}=0, \Sigma M_{y^{\prime}}=0, \Sigma M_{z^{\prime}}=0
\end{gathered}
$$
Because these are static bodies, the right side of the equations equal 0. In dynamics, they will equal the mass times the acceleration for translation and rotation.
For a rigid body in static equilibrium, that is a non-deformable body where forces are not concurrent, the sum of both the forces and the moments acting on the body must be equal to zero. The addition of moments (as opposed to particles where we only looked at the forces) adds another set of possible equilibrium equations, allowing us to solve for more unknowns as compared to particle problems.
Moments, like forces, are vectors. This means that our vector equation needs to be broken down into scalar components before we can solve the equilibrium equations. In a two dimensional problem, the body can only have clockwise or counter clockwise rotation (corresponding to rotations about the z axis). This means that a rigid body in a two dimensional problem has three possible equilibrium equations; that is, the sum of force components in the x and y directions, and the moments about the z axis. The sum of each of these will be equal to zero.
For a two dimensional problem, we break our one vector force equation into two scalar component equations.
$$\sum\vec F=0\\\sum F_x=0\:\sum F_y=0$$
The one moment vector equation becomes a single moment scalar equation.
$$\sum\vec M=0\\\sum M_z=0$$
If we look at a three dimensional problem we will increase the number of possible equilibrium equations to six. There are three equilibrium equations for force, where the sum of the components in the x, y, and z direction must be equal to zero. The body may also have moments about each of the three axes. The second set of three equilibrium equations states that the sum of the moment components about the x, y, and z axes must also be equal to zero.
We break the forces into three component equations
$$\sum\vec F=0\\\sum F_x=0\:\sum F_y=0\:\sum F_z=0$$
We break the moments into three component equations
$$\sum\vec M=0\\\sum M_x=0\:\sum M_y=0\:\sum M_z=0$$
Finding the Equilibrium Equations:
As with particles, the first step in finding the equilibrium equations is to draw a free body diagram of the body being analyzed. This diagram should show all the force vectors acting on the body. In the free body diagram, provide values for any of the known magnitudes, directions, and points of application for the force vectors and provide variable names for any unknowns (either magnitudes, directions, or distances).
Next you will need to choose the x, y, z axes. These axes do need to be perpendicular to one another, but they do not necessarily have to be horizontal or vertical. If you choose coordinate axes that line up with some of your force vectors you will simplify later analysis.
Once you have chosen axes, you need to break down all of the force vectors into components along the x, y and z directions (see the vectors page in Appendix 1 page for more details on this process). Your first equation will be the sum of the magnitudes of the components in the x direction being equal to zero, the second equation will be the sum of the magnitudes of the components in the y direction being equal to zero, and the third (if you have a 3D problem) will be the sum of the magnitudes in the z direction being equal to zero.
Next you will need to come up with the the moment equations. To do this you will need to choose a point to take the moments about. Any point should work, but it is usually advantageous to choose a point that will decrease the number of unknowns in the equation. Remember that any force vector that travels through a given point will exert no moment about that point. To write out the moment equations simply sum the moments exerted by each force (adding in pure moments shown in the diagram) about the given point and the given axis (x, y, or z) and set that sum equal to zero. All moments will be about the z axis for two dimensional problems, though moments can be about x, y and z axes for three dimensional problems.
Once you have your equilibrium equations, you can solve these formulas for unknowns. The number of unknowns that you will be able to solve for will again be the number or equations that you have.
Source: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/3_equilibrium_rigid_body/3-6_equilibrium_equations_rigid_body/equilibrium_equations_rigid_body.html
Here is a visual example of using the equilibrium equations:
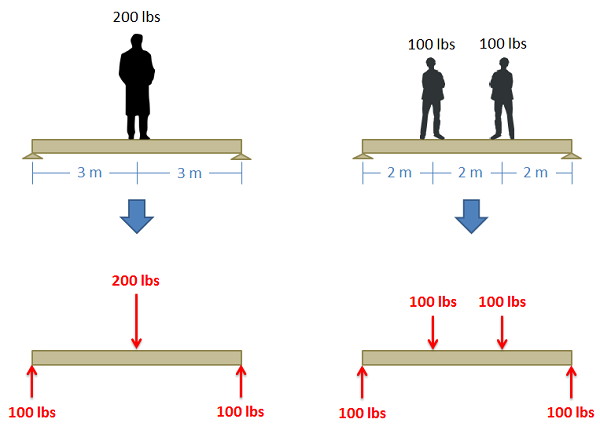
If we only consider the y (vertical) direction, the 200 lbs pushing down on the beam must be balanced by the reaction forces pushing up. The two reaction forces are equivalent because the forces on top are balanced evenly between the reaction forces. If they are at different locations, we use the sum of the moments equation and the distances of the people to determine the size of the reaction forces.
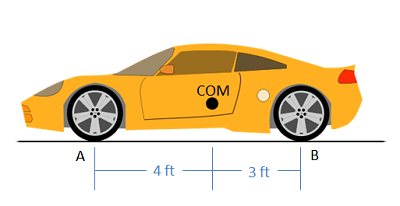
Example 1:
The car below has a mass of 1500 lbs with the center of mass 4 ft behind the front wheels of the car. What are the normal forces on the front and the back wheels of the car?
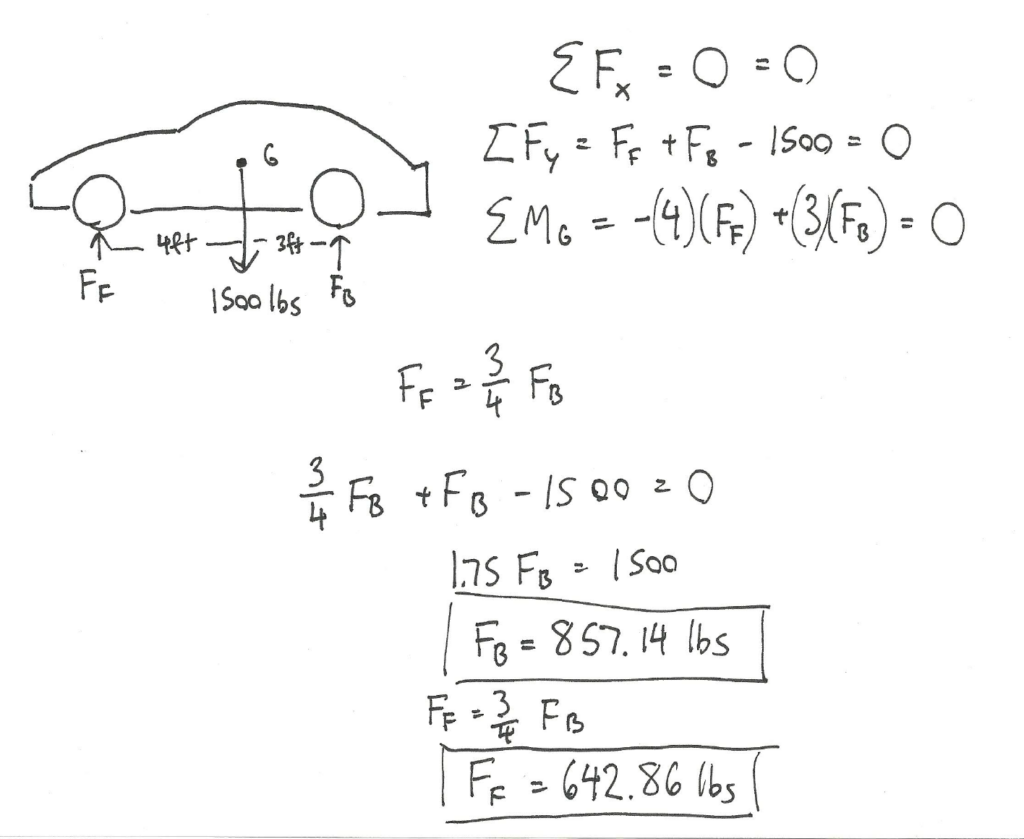
Source: Engineering Mechanics, Jacob Moore et al., http://mechanicsmap.psu.edu/websites/3_equilibrium_rigid_body/3-6_equilibrium_equations_rigid_body/pdf/EquilibriumEquationsExtended_WorkedProblem1.pdf
Example 2:
While sitting in a chair, a person exerts the forces in the diagram below. Determine all forces acting on the chair at points A and B. (Assume A is frictionless and B is a rough surface).
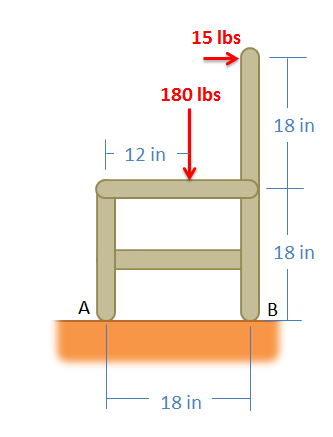
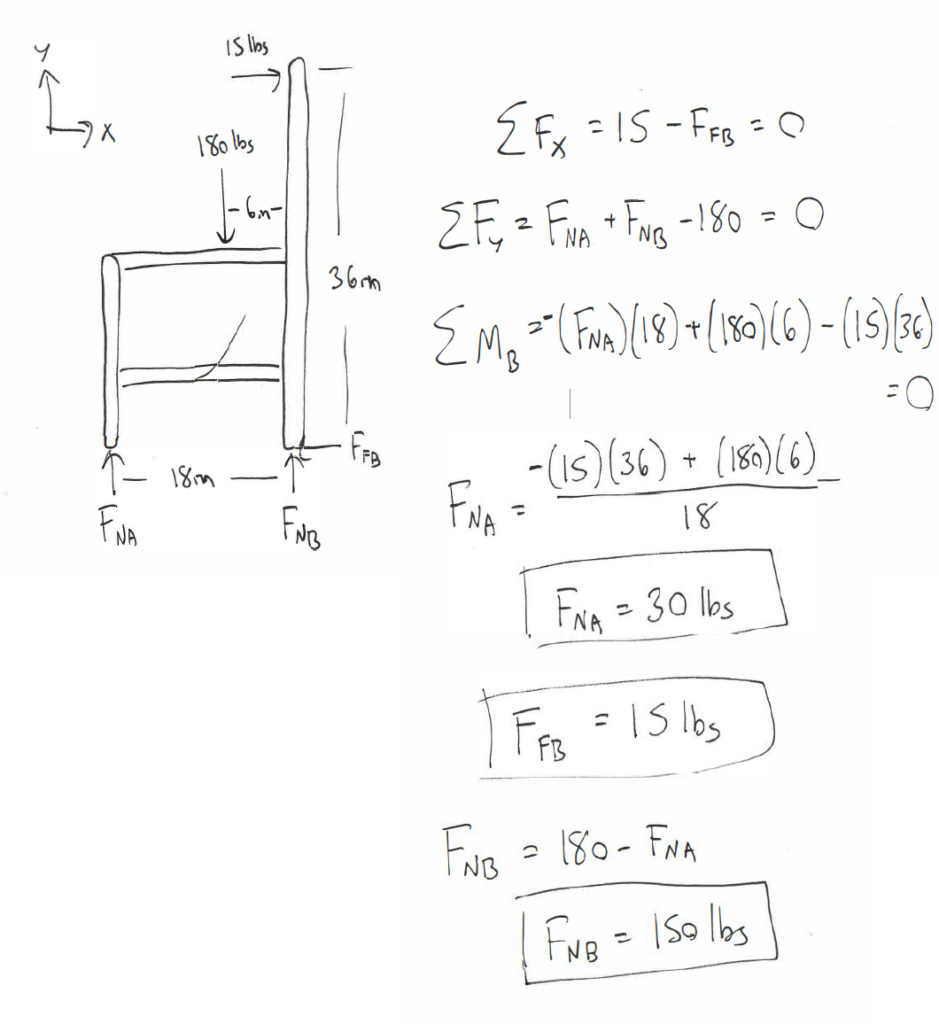
Source: Engineering Mechanics, Jacob Moore et al., http://mechanicsmap.psu.edu/websites/3_equilibrium_rigid_body/3-6_equilibrium_equations_rigid_body/pdf/EquilibriumEquationsExtended_WorkedProblem5.pdf
Key Takeaways
Basically: The equilibrium equations for rigid bodies are a way to determine unknown forces and moments using known forces and moments, separating the motion in 2 (or 3) directions for translation and rotation. Moments could be calculated because rigid bodies also consider shape and length.
Application: Calculate the reaction forces from the combined weight of an object.
Looking Ahead: This method will be used extensively in Ch 5 and 6.

