Chapter 4: Rigid Bodies
4.4 Friction and Impending Motion
Dry Friction
Dry friction is the force that opposes one solid surface sliding across another solid surface. Dry friction always opposes the surfaces sliding relative to one another and can have the effect of either opposing motion or causing motion in bodies.
The most commonly used model for dry friction is coulomb friction. This type of friction can further be broken down into static friction and kinetic friction. These two types of friction are illustrated in the diagram below. First imagine a box sitting on a surface. A pushing force is applied parallel to the surface and is constantly being increased. A gravitational force, a normal force, and a frictional force are also acting on the box.
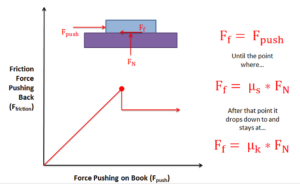
Static friction occurs prior to the box slipping and moving. In this region, the friction force will be equal in magnitude and opposite in direction to the pushing force itself. As the magnitude of the pushing force increases, so does the magnitude of the friction force.
If the magnitude of the pushing force continues to rise, eventually the box will begin to slip. As the box begins to slip, the type of friction opposing the motion of the box changes from static friction to what is called kinetic friction. The point just before the box slips is known as impending motion. This can also be thought of as the maximum static friction force before slipping. The magnitude of the maximum static friction force is equal to the static coefficient of friction times the normal force existing between the box and the surface. This coefficient of friction is a property that depends on both materials and can usually be looked up in tables.
Kinetic friction occurs beyond the point of impending motion when the box is sliding. With kinetic friction, the magnitude of the friction force opposing motion will be equal to the kinetic coefficient of friction times the normal force between the box and the surface. The kinetic coefficient of friction also depends upon the two materials in contact, but will almost always be less than the static coefficient of friction.
Source: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/7_friction/7-1_dry_friction/dryfriction.html
Slipping vs. Tipping
Imagine a box sitting on a rough surface as shown in the figure below. Now, imagine that we start pushing on the side of the box. Initially, the friction force will resist the pushing force, and the box will sit still. As we increase the force pushing the box, however, one of two things will occur.
- The pushing force will exceed the maximum static friction force, and the box will begin to slide across the surface (slipping).
- Or, the pushing force and the friction force will create a strong enough couple that the box will rotate and fall on its side (tipping).
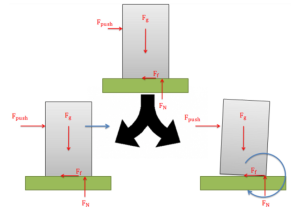
When we look at cases where either slipping or tipping may occur, we are usually interested in finding which of the two options will occur first. To determine this, we usually determine both the pushing force necessary to make the body move and the pushing force necessary to make the body tip over. Whichever option requires less force is the option that will occur first.
Determining the Force Required to Make an Object “Slip”:
A body will slide across a surface if the pushing force exceeds the maximum static friction force that can exist between the two surfaces in contact. As in all dry friction problems, this limit to the friction force is equal to the static coefficient of friction times the normal force between the body. If the pushing force exceeds this value, then the body will slip.
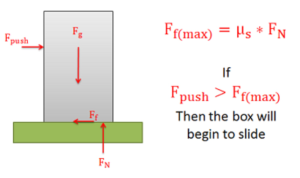
Determining the Force Required to Make an Object “Tip”:
The normal forces supporting bodies are distributed forces. These forces will not only prevent the body from accelerating into the ground due to gravitational forces, but they can also redistribute themselves to prevent a body from rotating when forces cause a moment to act on the body. This redistribution will result in the equivalent point load for the normal force shifting to one side or the other. A body will tip over when the normal force can no longer redistribute itself any further to resist the moment exerted by other forces (such as the pushing force and the friction force).
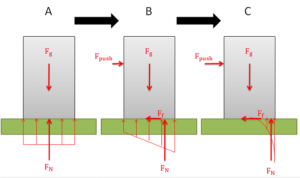
The easiest way to think about the shifting normal force and tipping is to imagine the equivalent point load of the distributed normal force. As we push or pull on the body, the normal force will shift to the left or right. This normal force and the gravitational force create a couple that exerts a moment. This moment will be countering the moment exerted by the couple formed by the pushing force and the friction force.
Because the normal force is the direct result of physical contact, we cannot shift the normal force beyond the surfaces in contact (aka. the edge of the box). If countering the moment exerted by the pushing force and the friction force requires shifting the normal force beyond the edge of the box, then the normal force and the gravity force will not be able to counter the moment, and as a result, the box will begin to rotate (aka tip over).
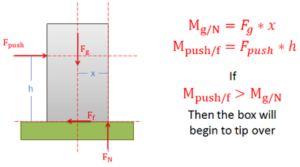
Source: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/7_friction/7-2_slipping_vs_tipping/slippingvstipping.html
Example 1
The box shown below is pushed as shown. If we keep increasing the pushing force, will the box first begin to slide, or will it tip over?
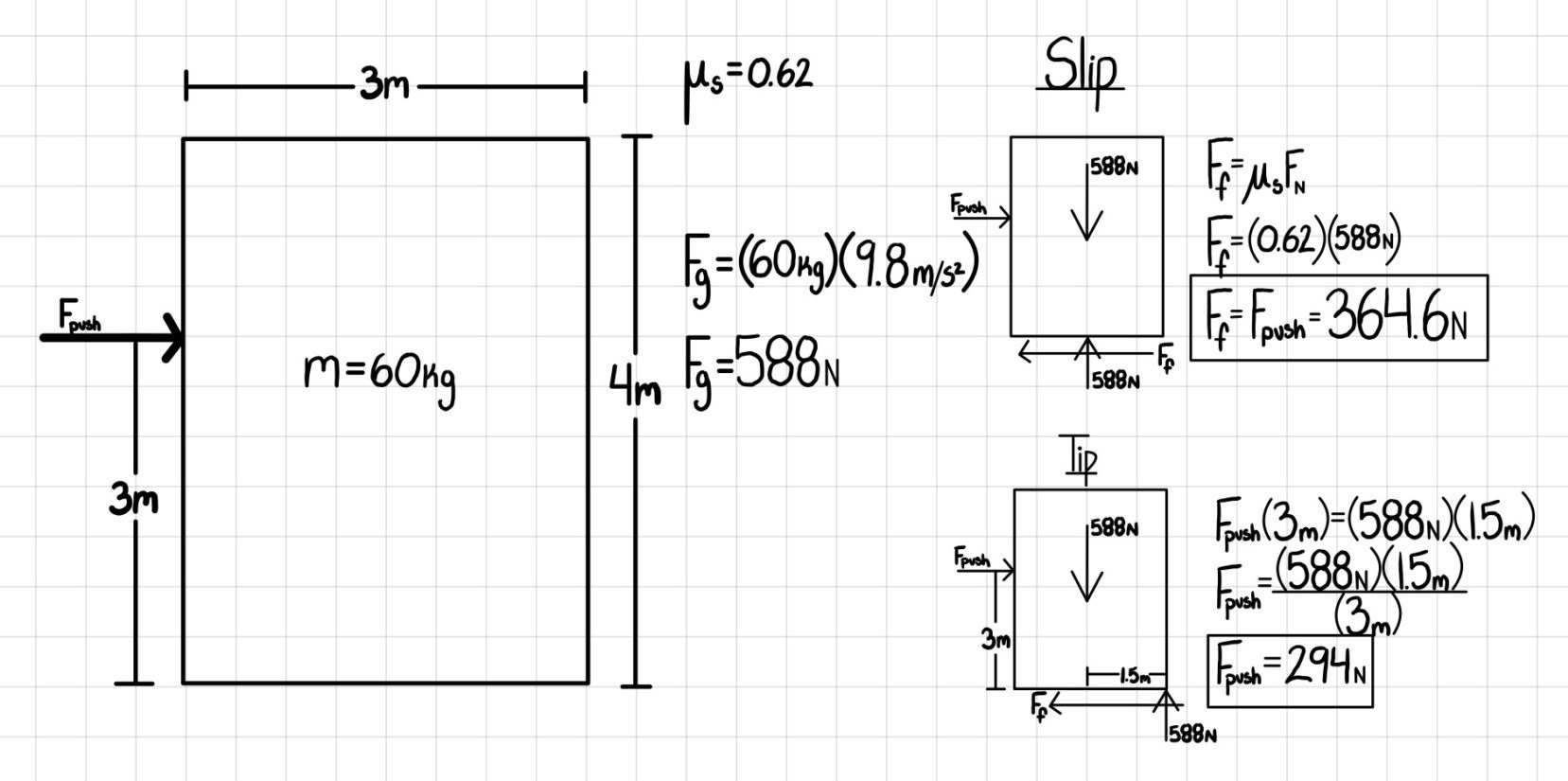
Therefore, the box will TIP first.
Source: Gayla Cameron.
Example 2:
A 500 lb box is sitting on a concrete floor. If the static coefficient of friction is .7 and the kinetic coefficient of friction is .6:
- What is the friction force if the pulling force is 150 lbs?
- What pulling force would be required to get the box moving?
- What is the minimum force required to keep the box moving once it has started moving?

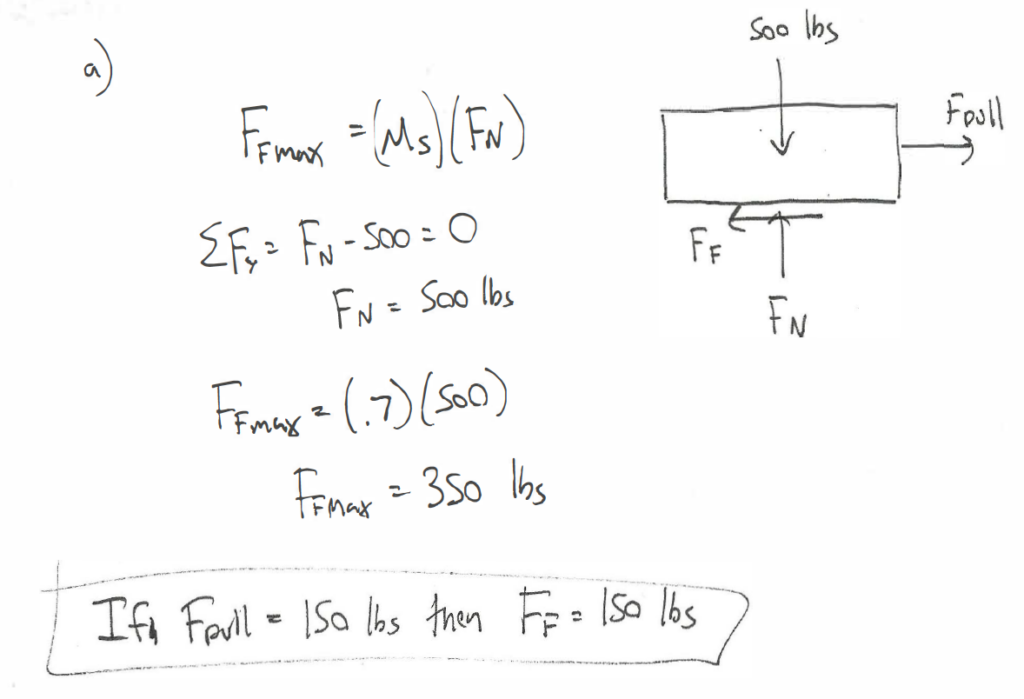
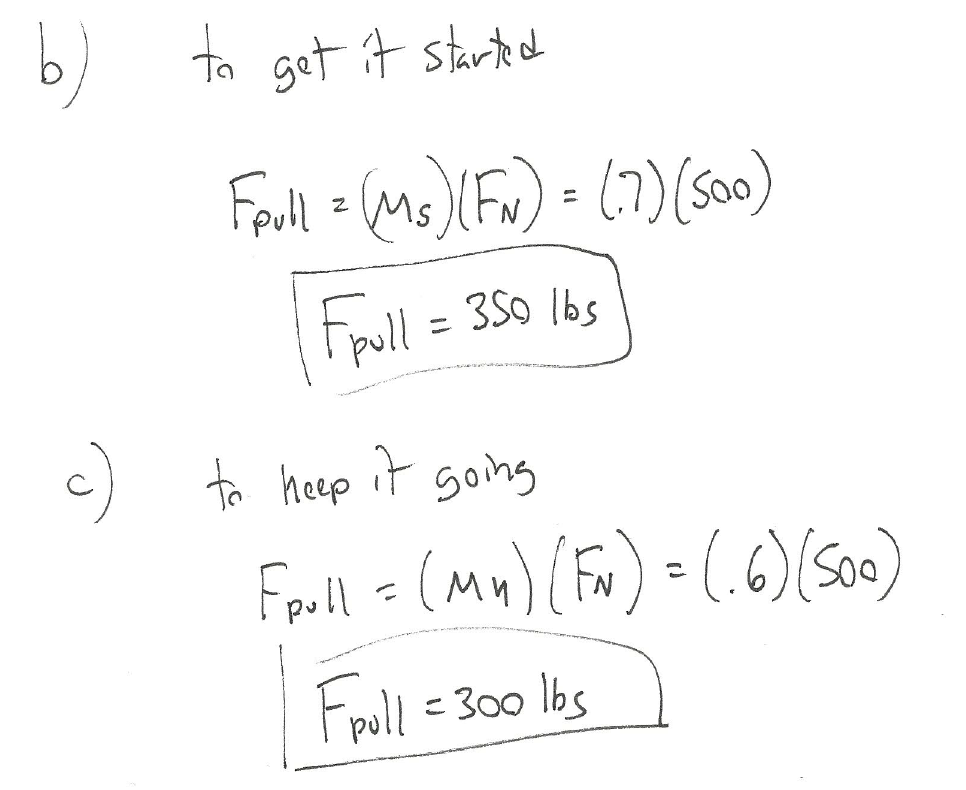
Source: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/7_friction/7-1_dry_friction/pdf/DryFriction_WorkedExample1.pdf
Example 3:
A 30 lb sled is being pulled up an icy incline of 25 degrees. If the static coefficient of friction between the ice and the sled is .4 and the kinetic coefficient of friction is .3, what is the required pulling force needed to keep the sled moving at a constant rate?
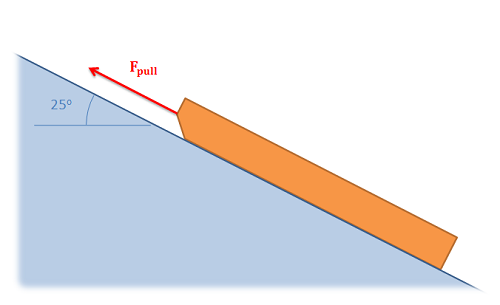
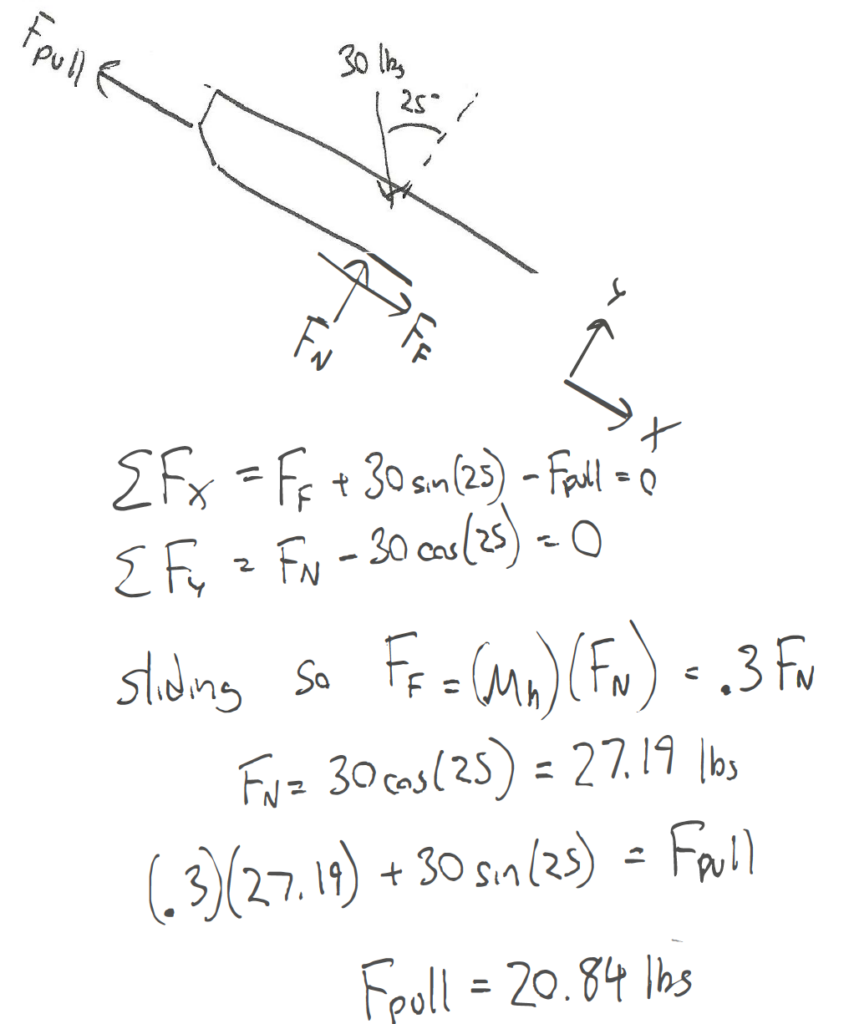
Source: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/7_friction/7-1_dry_friction/pdf/DryFriction_WorkedExample2.pdf
Example 4:
A plastic box is sitting on a steel beam. One end of the steel beam is slowly raised, increasing the angle of the surface until the box begins to slip. If the box begins to slip when the beam is at an angle of 41 degrees, what is the static coefficient of friction between the steel beam and the plastic box?
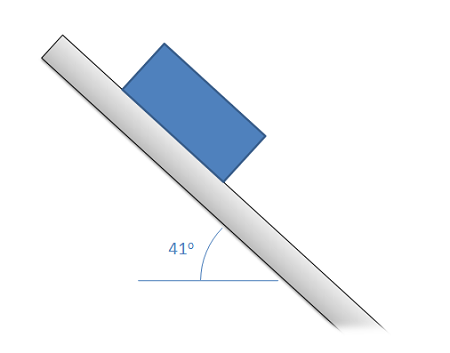
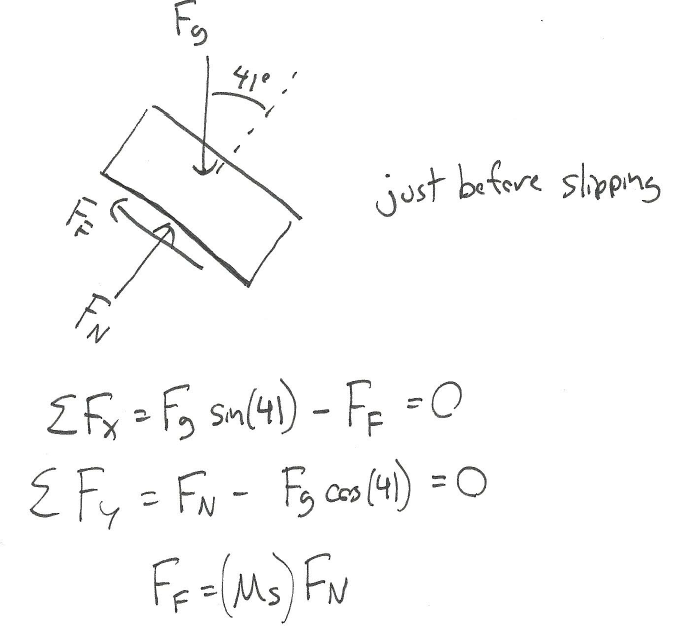
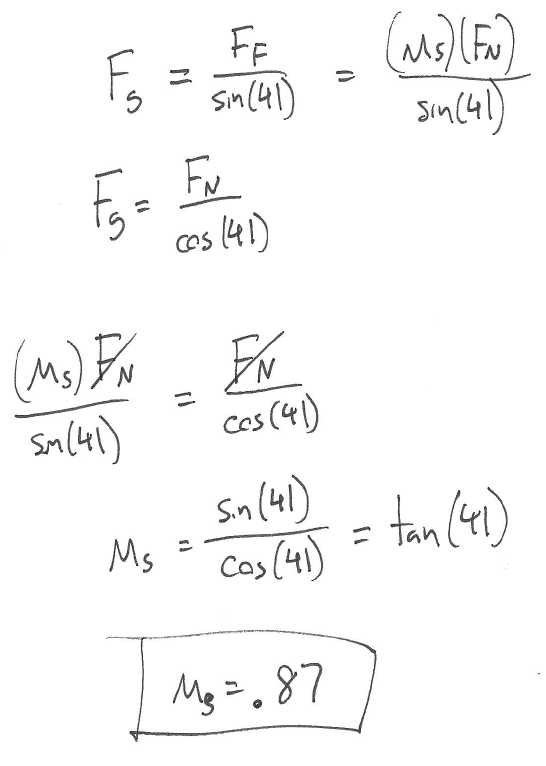
Source: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/7_friction/7-1_dry_friction/pdf/DryFriction_WorkedExample3.pdf
Example 5: Slipping vs Tipping
Explanation: If it’s tipping, all of the normal force will be at the corner. If it starts slipping, it must overcome the static frictional force. Comparing the pushing force needed to tip or slip, the pushing force is lower to cause tipping occurs than the pushing force to cause slipping, there fore it will tip first.
The box shown below is pushed as shown. If we keep increasing the pushing force, will the box first begin to slide or will it tip over?
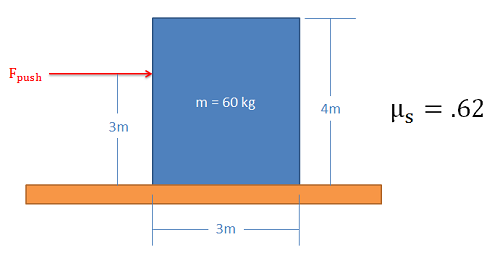
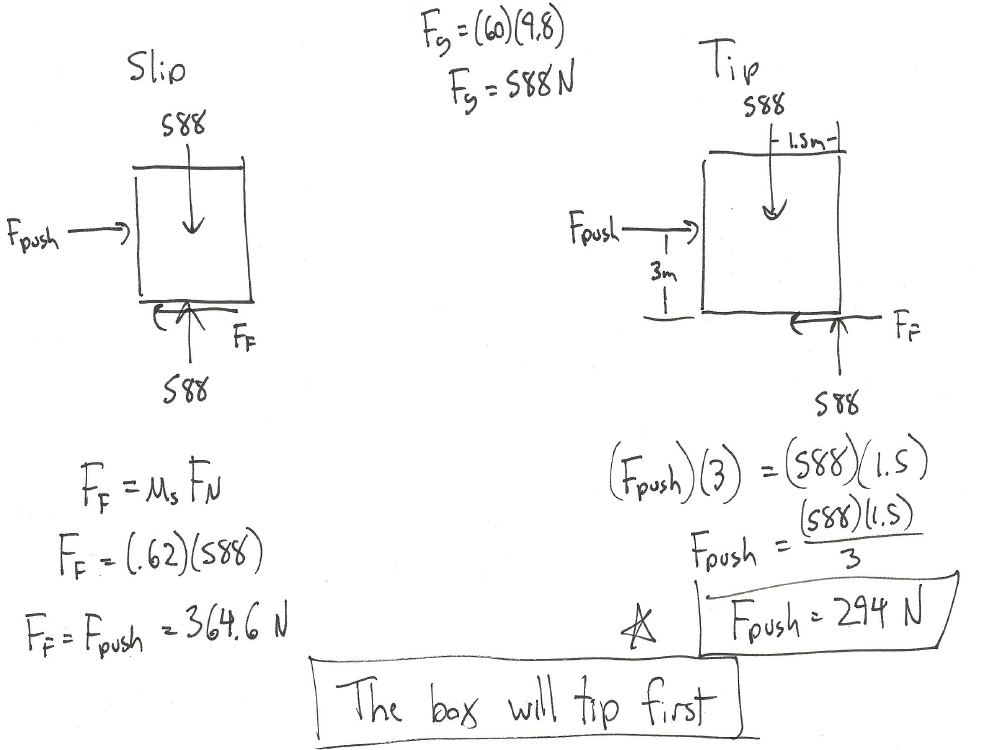
Source: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/7_friction/7-2_slipping_vs_tipping/pdf/TippingVsSlipping_WorkedExample1.pdf
Key Takeaways
Basically, Friction always opposes motion. The coefficient of static friction is always higher than the coefficient of kinetic friction.
Application: Slipping and tipping are interesting cases, looking at friction. Depending on the mass, the height of the applied force, and the frictional surface, you can calculate whether the object will tip or slip first.
Looking Ahead: This will become important in Dynamics.

