Chapter 1: Fundamental Concepts
1.8 Examples
Here are examples from Chapter 1 to help you understand these concepts better. These were taken from the real world and supplied by FSDE students in Summer 2021. If you’d like to submit your own examples, please send them to:
eosgood@upei.ca
Example 1.8.1: Vectors, Submitted by Tyson Ashton-Losee
1. Problem
After a long day of studying, a student sitting at their computer moves the cursor from the bottom left of the screen to the top right in order to close a web browser. The computer mouse was displaced 6 cm along the x-axis and 3.5 cm along the y-axis. Draw the resultant vector and calculate the distance traveled.

2. Draw
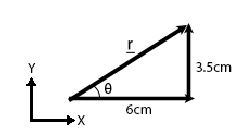
3. Knowns and Unknowns
Known:
- x = 6 cm
- y = 3.5 cm
Unknown:
- r
- θ
4. Approach
Use SOH CAH TOA, first find θ, then r
5. Analysis
[latex]\begin{aligned} &\tan \theta=\frac{y}{x} \\ &\tan \theta=\frac{3.5 \mathrm{~cm}}{6 \mathrm{~cm}} \\ &\theta=\tan ^{-1}\left(\frac{3.5}{6}\right) \\ &\theta=30.256^{\circ} \\ &\sin \theta=\frac{y}{r} \\ &r=\frac{y}{\sin \theta} \\ &r=\frac{3.5 \mathrm{~cm}}{\sin \left(30.256^{\circ}\right)} \\ &r=6.946 \mathrm{~cm} \\ &r=6.9 \mathrm{~cm} \end{aligned}[/latex]
6. Review
It makes sense that the angle is less than 45, because y is smaller than x. Also, if you use the Pythagorean theorem to find r, you get the same answer.
Example 1.8.2: Vectors, Submitted by Brian MacDonald
1. Problem
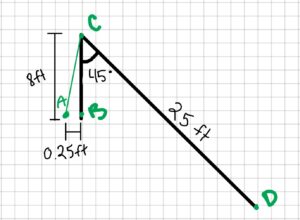
Mark is fishing in the ocean with his favourite fishing rod. The distance between the tip of the rod and the reel is 8 ft and the length of the reel handle is 0.25 ft. The angle between the fishing rod and fishing line is 45 degrees. If Mark catches a fish when 25 ft of the fishing line is released while the fish is diving down with a force of 180 N, how much force does Mark need to apply (push down) to the reel handle to bring in the fish? Draw the position vector of the fish relative to the reel.
Assumptions:
- Mark can reel in the fish when he generates more torque with the handle than the amount of torque that the fish is applying to the reel while pulling on the line.
- The fishing line comes out of the reel in a straight line at a 90-degree angle.

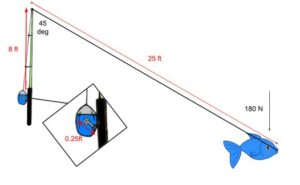
2. Draw
Sketch:
Free-body diagram:
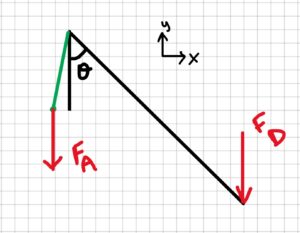
3. Knowns and Unknowns
Known:
- rAB = 0.25 ft
- rBC = 8 ft
- rCD = 25 ft
- FD = 180 N
- θ = 45°
Unknown:
- FA
- vector rAD
4. Approach
Convert inches to meters, then use the equation below.
[latex]T=|r| *|F| * \sin \theta\\[/latex]
5. Analysis
Step 1: Convert inches to meters
[latex]\begin{align} &25 \mathrm{ft} * \frac{12 \mathrm{in}}{1 \mathrm{ft}} * \frac{2.54 \mathrm{cm}}{\operatorname{1in} } * \frac{\operatorname{1m}}{100 \mathrm{cm}}=7.62 \mathrm{m}\\\\ &\quad\mathrm{and}\\\\ &0.25 \mathrm{ft} * \frac{12 \mathrm{in}}{1\mathrm{ft}} * \frac{2.54 \mathrm{cm}}{\operatorname{1in} } * \frac{\mathrm{1m}}{100 \mathrm{cm}}=0.0762 \mathrm{m}\\ \end{align}[/latex]
Step 2: Solve for TD
[latex]\begin{aligned}&T_{D}=\left|r_{C D}\right| * \left|F_{D}\right| * \sin \theta\\ &T_{D}=(7.62 m)(180 N) \sin \left(45^{\circ}\right)\\ &T_{D}=969.86766 \mathrm{Nm} \end{aligned}[/latex]
Step 3: Solve for FA
[latex]\begin{aligned}&T_{A}=\left|r_{AB}\right| * \left|F_{A}\right| * \sin \theta\\ &\text { Assume } T_{A}=T_{D}\\ &F_{A}=\frac{T_{D}}{\left|r_{AB}\right| * \sin \theta} \\ &F_{A}=\frac{969.86766 \mathrm{ Nm}}{0.0762 \mathrm{~m} * \sin \left(90^{\circ}\right)} \\ &F_{A}=12 727.9 \mathrm{N} \\ &F_{A}=13 000 \mathrm{N} \end{aligned}[/latex]
Vector rAD:
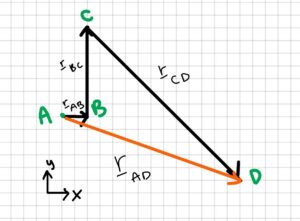
[latex]\begin{aligned} &\vec r_{A D}=\vec r_{A B}+\vec r_{B C}+\vec r_{C D} \\ &\vec {r}_{A D}=\left[\begin{array}{c} 0.25 \\ 0 \end{array}\right] f t+\left[\begin{array}{l} 0 \\ 8 \end{array}\right] f t+\left[\begin{array}{c} 25 \sin 45^{\circ} \\ -25 \cos 45^{\circ} \end{array}\right] f t \\ &\vec r_{A D}=\left[\begin{array}{cc} 17.93 \\ -9.68 \end{array}\right] ft \end{aligned}[/latex]
6. Review
Though yielding a very large number, the answer appears correct from the information given. 13,000 N of force is the amount of force Mark would need to apply to the reel handle to generate the same amount of force that the fish creates. 13,000 N in reality is too much for one to generate, but also in a real scenario, one would not have to generate the same amount of force to reel in the fish, to reel gearing, the amount of torque generated by the fishing rod itself, etc. In other words 13 000 N of force is too high in a real scenario, but with the assumptions given in the problem, the number seems reasonable. The answer also has the correct unit, N.
Example 1.8.3: Dot product and cross product, submitted by Anonymous ENGN 1230 Student
1. Problem
[latex]\underline{a}=[6\;\;\;5\;\;\;3]\;\;\;\underline{b}=[8\;\;\;1\;\;\;3][/latex]
a) Find 6a
b) Find [latex]a\cdot b[/latex]
c) Find [latex]a\times b[/latex]
d) Find [latex]2a\times b[/latex]
2. Draw
N/A
3. Knowns and Unknowns
Known:
- a
- b
Unknowns:
- 6a,
- [latex]a\cdot b[/latex]
- [latex]a\times b[/latex]
- [latex]2a\times b[/latex]
4. Approach
Use dot product and cross product equations
5. Analysis
Part a:
[latex]6\underline{a}=6*[6\;\;\;5\;\;\;3]\\6\underline{a}=[36\;\;\;30\;\;\;18][/latex]
Part b:
[latex]\underline{a}\cdot\underline{b}=[6\;\;\;5\;\;\;3]\cdot[8\;\;\;1\;\;\;3]\\=6\cdot 8+5\cdot 1+3\cdot3\\=48+5+9\\\underline{a}\cdot\underline{b}=62[/latex]
Part C:
[latex]\underline{a}\times\underline{b}=\begin{bmatrix} \underline{\hat{i}} &\underline{\hat{j}} & \underline{\hat{k}} \\ 6 & 5 & 3 \\ 8 & 1 & 3 \end{bmatrix}\\(5\cdot 3-3\cdot 1)\underline{\hat{i}}-(6\cdot 3-3\cdot 8)\underline{\hat{j}}+(6\cdot 1-5\cdot 8)\underline{\hat{k}}\\\underline{a}\times\underline{b}=12\underline{\hat{i}}+6\underline{\hat{j}}-34\underline{\hat{k}}[/latex]
Part D:
[latex]2\underline{a}=2*[6\;\;\;5\;\;\;3]=[12\;\;\;10\;\;\;6]\\\underline{b}=[8\;\;\;1\;\;\;3]\\2\underline{a}\times\underline{b} = \begin{bmatrix} \underline{\hat{i}} & \underline{\hat{j}} & \underline{\hat{k}} \\ 12 & 10 & 6 \\ 8 & 1 & 3 \end{bmatrix} \\=(10\cdot 3-6\cdot 1)\underline{\hat{i}}-(12\cdot 3-6\cdot 8)\underline{\hat{j}}+(12\cdot 1-10\cdot 8)\underline{\hat{k}}\\2\underline{a}\times\underline{b}=24\underline{\hat{i}}+12\underline{\hat{j}}-68\underline{\hat{k}}[/latex]
6. Review
The answer to part d is double the answer for part c, which makes sense. It also makes sense that the answers to a, c, and d have values in three directions, while b only has magnitude.
Example 1.8.4: Torque, Submitted by Luke McCarvill
1. Problem
To start riding her bicycle, Jane must push down on one of her bike’s pedals, which are on 16-centimetre-long crank arms. Jane can push directly downwards with her legs with a force of 100N. Jane notices that the pedal’s starting position can sometimes make it more or less useful in generating torque.
a) What is the ideal angle that Jane’s bike pedal should be at in order to generate the most torque? Prove this mathematically. (Assume we only care about the very start of her very first push, and choose a reference frame for the angle that makes most sense for you.)
b) What angle(s) should the bike pedal be at if Jane wants to generate exactly half of the maximum amount of torque?
c) Is there any position(s) at which the pedal will create zero torque? Where are they and why?


2. Draw
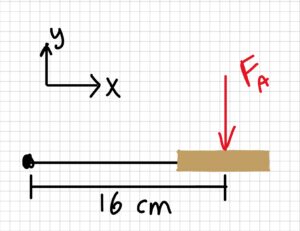
3. Knowns and Unknowns
Knowns:
[latex]\begin{aligned} &\vec r=\left[\begin{array}{c} 0.16 \\ 0 \\ 0 \end{array}\right] m \\ &\vec F_{A}=\left[\begin{array}{c} 0 \\ -100 \\ 0 \end{array}\right] N \end{aligned}[/latex]
Unknowns:
- position of r for maximum torque
- position of r for half of the maximum torque
- position of r for zero torque, and why
4. Approach
For part a), I will find a general equation for torque based on the given values in terms of θ, then analyze the function for its maxima
For part b), I will find the magnitude of 50% of maximum torque and then reverse-engineer the equation to determine what angle(s) the pedal needs to be at to satisfy the equation.
For part c), I will look back at my equation and find when the equation equals zero, then try to understand why, given the example problem.
5. Analysis
Part a:
[latex]\begin{aligned} &T=\left|\vec F_{A}\right| * \left|\vec r\right| * \sin \theta \\ &T=(100 N) *(0.16 m) * \sin \theta \\ &T=16 \sin \theta \mathrm{Nm} \\ &\quad\left\{90^{\circ}+360^{\circ} k ; k \in \mathbb{Z}\right\} \end{aligned}[/latex]
Thinking about the shape of the sine function in the first period, the maximum occurs at 90 degrees.
You could say algebraically that the maximum is at 90, 450, 810, etc., but these angles all represent the same position on the wheel. Therefore, we will use 90.
Part b:
[latex]\begin{aligned} &T_1=\left|F_{A}\right| *|r| * \sin \theta \\ &T_1=(100 N)*(0.16 m)* \sin 90^{\circ} \\ &T_1=16 N m \end{aligned}[/latex]
Find 50% of the maximum torque:
[latex]T_2=\frac{T_1}{2}[/latex]
[latex]\frac{16 Nm}{2}=8 Nm[/latex]
Rearrange T2 equation: [latex]T_{2}=\left|F_{A}\right| *|{r}| \sin \theta[/latex]
[latex]\begin{aligned}&\sin \theta=\frac{T_{2}}{\left| F_{A}\right| * \left| r \right|} \\ &\sin \theta=\frac{8 N m}{(100 N)*(0.16 m)} \\ &\sin \theta=0.5 \\ &\theta=30^{\circ}, 150^{\circ}, etc \end{aligned}[/latex]
Therefore, Jane could push at 30 from vertical, or 150 from vertical to create half the torque.
*Interesting to note is that half the angle does not yield half the torque; the angle is 30, not 45. This is because the sine function is nonlinear.*
Part C:
T = 16 sinθ tells us that the angles of 0 and 180 will give us zero torque.
This makes sense given that pushing straight down on a stable pendulum will not cause the pendulum to rotate!
Likewise, if you just stand on your pedals, you’re providing lots of downward force, but creating zero torque since the crank arm and the direction of the force are parallel (or antiparallel)!
6. Review
These answers have the correct units (Nm and degrees) and are within a reasonable order of magnitude based on the given information. See logic/explanations above for more details.
Example 1.8.5: Torque, submitted by Hamza Ben Driouech
1. Problem
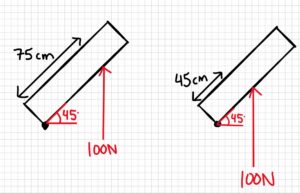
A person is pushing on a door with a force of 100 N. The door is at an angle α = 45° as shown in the sketch below.
a) Calculate the moment when r is 45 cm and 75 cm.
b) At what angle(s) is the moment zero? Explain why.
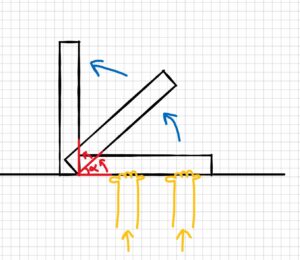
Assumptions: Model the force as a single point load acting on the door.
2. Draw
Sketch:
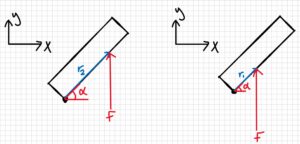
Free-body diagram:
3. Knowns and Unknowns
Knowns:
- F = 100N
- r1 = 45cm
- r2 = 75cm
- α = 45°
Unknowns:
- M1
- M2
- Angle when M is zero
4. Approach
Use the equation below.
[latex]M=|r|\cdot|F|\cdot\sin\theta[/latex]
5. Analysis
Part a)
The angle we were given is not technically the one we should use in the moment equation. The angle should be between r and F. Therefore, we have to find the new angle.
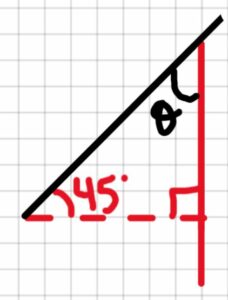
As shown below, the angle we find is also 45°. Now we can continue and solve for M1 and M2.
[latex]\theta=90^{\circ}-45^{\circ}[/latex]
[latex]\theta=45^{\circ}[/latex]
[latex]M_1=|r_1|\cdot|F|\cdot\sin\theta\\M_1=0.45m\cdot 100N\cdot\sin(45^{\circ})\\m_1=31.82Nm\\\\M_2=|r_2|\cdot |F|\cdot\sin\theta\\M_2=0.75m\cdot 100N\cdot\sin(45^{\circ})\\M_2=53.03Nm[/latex]
Part b)
[latex]M=|r|\cdot|F|\cdot\sin\theta\\if \sin\theta=0, M=0\\\sin\theta=0\\\theta=\sin^{-1}(0)\\\theta=0^{\circ}, 180^{\circ}, 360^{\circ}[/latex]
Answer: The moment is zero when the angle between the force and the moment arm is 0° or 180° (360 would represent the same angle as 0°, as would 540°, etc.)
6. Review
It makes sense that the moment is zero when the door is either closed or wide open, because when we apply a force at those positions, no movement of the door is possible.
Example 1.8.6: Bonus Vector Material, Submitted by Liam Murdock
1. Problem
George travelled a displacement of dg = [7 0 8] m from his car. George’s dog, named Sparky, on the other hand, travelled a displacement of ds = [0 6 6] m from George’s car. George called Sparky’s name, and the dog ran to George’s position. It took Sparky four seconds to get there.
- What is the displacement from George to his dog?
- What is Sparky’s velocity? (No need to draw.)
- What is Sparky’s speed? (No need to draw.)

2. Draw
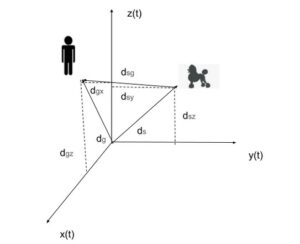
3. Knowns and Unknowns
Knowns:
- dg = [7 0 8] m
- ds = [0 6 6] m
- t= 4 seconds
Unknowns:
- vsg= ?
- dsg= ?
4. Approach
We are going to use vector operations (both subtraction and division), the velocity-displacement relationship, the velocity-speed relationship, and Pythagoras’ theorem to solve this problem.
5. Analysis
Part a:
[latex]d_{sg}=d_{g}-d_{s}[/latex]
[latex]d_{sg}=[7\;\;\;0\;\;\;8]m-[0\;\;\;6\;\;\;6]m[/latex]
[latex]d_{sg}=[7-0\;\;\;0-6\;\;\;8-6]m[/latex]
[latex]d_{sg}=[7\;\;\;-6\;\;\;2]m[/latex]
Part b:
[latex]v_{sg}=d_{sg}/t[/latex]
[latex]v_{sg}=[7\;\;\;-6\;\;\;2]m/4s[/latex]
[latex]v_{sg}=[7/4\;\;\;-6/4\;\;\;2/4]m/s[/latex]
[latex]v_{sg}=[1.75\;\;\;-1.5\;\;\;0.5]m/s[/latex]
Part C:
[latex]V_{sg}=\sqrt{V_{sgx}^2+V_{sgy}^2+V_{sgz}^2}[/latex]
[latex]V_{sg}=\sqrt{1.75^2+(-1.5)^2+0.5^2}[/latex]
[latex]V_{sg}=2.36m/s[/latex]
6. Review
Part a:
One way to review the question is to walk through the solution verbally. Our solution shows that for Sparky to get to George, he must walk 7 m in the positive x-direction (almost out of the page), 6 m in the negative y-direction (left), and finally 2 m in the positive z-direction (up).
Firstly, since the dog initially did not go in the x-direction, it makes sense that Sparky would have to copy George’s exact x movement. Secondly, since George did not move in the y-direction, it would make sense that Sparky would just have to retrace his steps, and if he initially went 6 m right, he would have to go 6 m left. Thirdly, George and Sparky both went upwards, but George went 2 m higher with an altitude of 8 m compared to Sparky’s 6 m, correlating to Sparky having to go positive 2 m in the z-direction to meet George.
Therefore, since all the movements make sense for Sparky to meet George (using logic), the answer is proven to be right.
Parts b and c:
Since B and C correlate to the same magnitude, they can be reviewed together. From a quick search, an average dog tops out at a speed of 19 miles per hour. We can convert this to SI units:
[latex]\frac{19 \text { miles }}{1 h r}\left(\frac{1 \mathrm{~km}}{0.621371 \text { miles }}\right)\left(\frac{1000 \mathrm{~m}}{1 \mathrm{~km}}\right)\left(\frac{1 \mathrm{hr}}{3600}\right)=8.49 \mathrm{~m} / \mathrm{s}[/latex]
The top speed of an average dog is 8.49 m/s. So 2.36m/s is approximately a quarter of the top speed of an average dog. Sparky probably was not sprinting at full speed and he could be a slower dog breed, making 2.36m/s a reasonable answer.
Example 1.8.7: Cross Product, Submitted By Victoria Keefe
Using the cross product, find the torque on point A due to force F. Force F = (5 i – 2 j + k)N. The width of the platform is 1 meter, the height is 0.25 meters, and the length is 5 meters.
2: Sketch
N/A
3. Knowns and Unknowns
Knowns:
- F = (5 i – 2 j + k)N
- l = 5m
- w = 1m
- h = 0.25m
Unknown:
- M
4: Approach
Use the equation: M = r x F
5. Analysis
[latex]r = (-1 \hat{i} + 0.25 \hat{j} + 5 \hat{k})m \\ \bar{F} = (5 \hat{i} - 2 \hat{j} + \hat{k})N \\ \bar{M} =[ [(0.25 \cdot 1) - (-2 \cdot 5)] \hat{i} - [(-1 \cdot 1) - (5 \cdot 5)] \hat{j} + [(-1 \cdot -2) - (5 \cdot 0.25)] \hat{k}]Nm \\ \bar{M} = (10.25 \hat{i} + 26 \hat{j} +0.75 \hat{k})Nm[/latex]
6.0 Review
The resulting moment has reasonable values and can be verified with a cross product calculator.

