Chapter 7: Inertia
7.6 Examples
Here are examples from Chapter 7 to help you understand these concepts better. These were taken from the real world and supplied by FSDE students in Summer 2021. If you’d like to submit your own examples, please send them to the author eosgood@upei.ca.
Example 7.6.1: All of Ch 7, Submitted by William Craine
1. Problem
A person is playing soccer. The ball they are using has a diameter of 20 cm and a mass of 0.45 kg. The person’s leg has a mass of 18 kg, and their foot has a mass of 8 kg. Assume that all the shapes have uniform density.
a) Find the cm for the ball.
b) Calculate the mass moment of inertia (MMOI) for the ball.
c) Find the cm for the person’s leg and foot.
d) Find the MMOI for the person’s leg and foot on the y-axis about A.

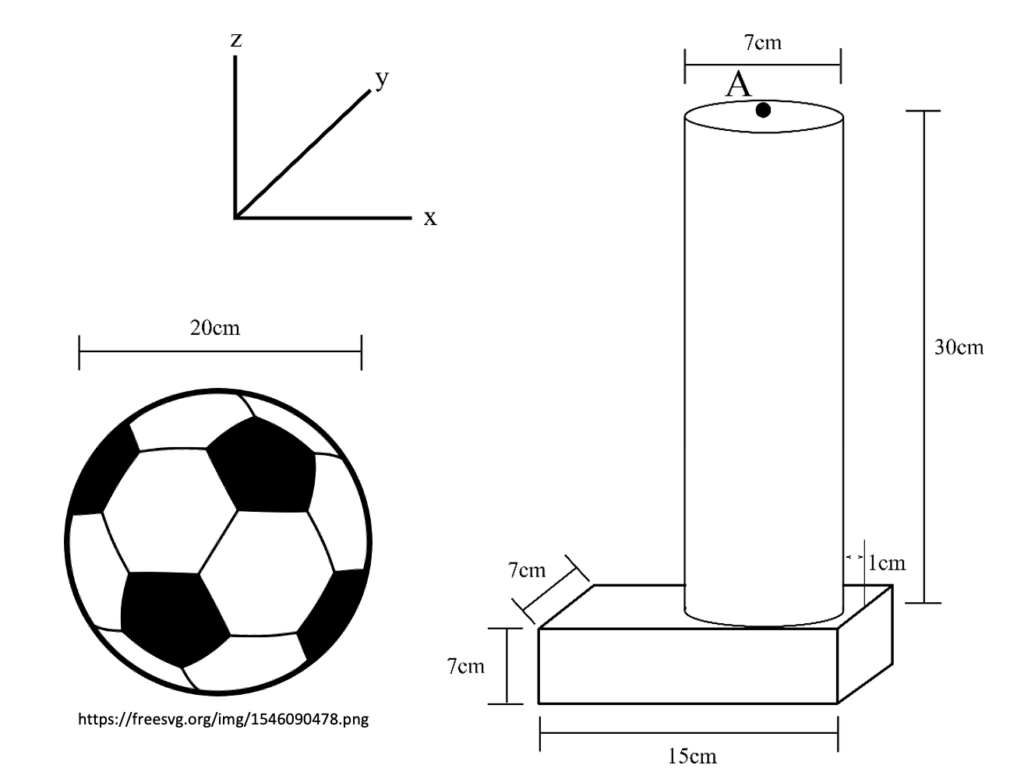
2. Draw
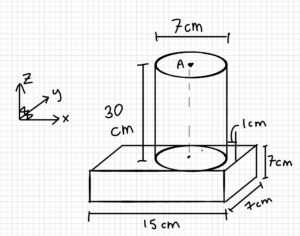
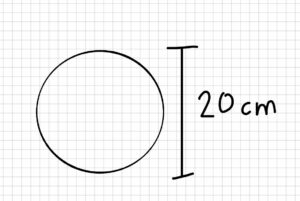
3. Knowns and Unknowns
Knowns:
- mb = 0.45 kg
- db = 20 cm
- mL = 18 kg
- mf = 8 kg
Unknowns:
- xb
- Ib
- xp
- Ip x
4. Approach
Find the cm for both objects using arbitrary coordinates since no origin is given.
Use the sphere MMOI formula for the ball.
Calculate the individual MMOIs for the leg and foot, then use the parallel axis theorem to get each shape’s MMOI about the system cm, add them, and then use the parallel axis theorem to get the MMOI about A.
5. Analysis
Part a (find the center of mass of the ball):
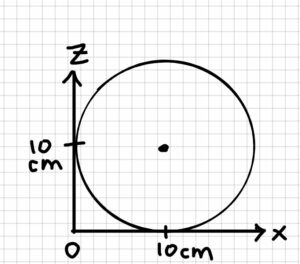
[latex]x_b=(10\underline{\hat{i}}+10\underline{\hat{j}}+10\underline{\hat{k}})cm[/latex]
Part b (find the MMOI of the ball about its center of mass):
[latex]I_{xx}=I_{yy}=I_{zz}=\frac{2}{3}mr^2\\\qquad \quad=\frac{2}{3}(0.45 kg)(0.1m)^2\\I_b=0.003kgm^2[/latex]
Part c (find the center of mass for the system of the person’s leg):
Step 1: Find the center of mass of the foot (f)
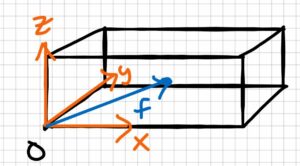
[latex]f=\frac{15cm}{2}\underline{\hat{i}}+\frac{7cm}{2}\underline{\hat{j}}+\frac{7cm}{2}\underline{\hat{k}}\\f=(7.5\underline{\hat{i}}+3.5\underline{\hat{j}}+3.5\underline{\hat{k}})cm[/latex]
Step 2: Find the center of mass of the leg (L)
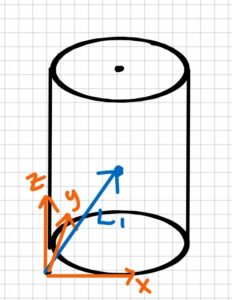
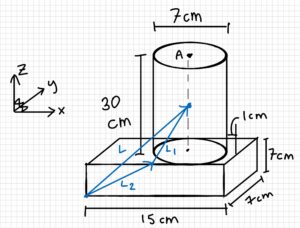
[latex]L_1=(3.5\underline{\hat{i}}+3.5\underline{\hat{j}}+15\underline{\hat{k}})cm\\L_2=(15cm-7cm-1cm)\underline{\hat{i}}+(0cm)\underline{\hat{j}}+(7cm)\underline{\hat{k}}\\\qquad \quad L_2 = (7 \underline{\hat{i}}+(0)\underline{\hat{j}}+(7)\underline{\hat{k}} )cm[/latex]
[latex]\\L=L_1+L_2\\L=(3.5cm+7cm)\underline{\hat{i}}+(3.5cm+0cm)\underline{\hat{j}}+(15cm+7cm)\underline{\hat{k}}\\L=(10.5\underline{\hat{i}}+3.5\underline{\hat{j}}+22\underline{\hat{k}})cm[/latex]
Step 3: find the center of mass of the system (P)
[latex]x_p=\frac{\sum m_i x_i}{\sum m_i}\\X_p=\frac{m_f\cdot x_f+m_L\cdot x_L}{m_f+m_L}\\x_p=\frac{8kg\cdot 7.5cm+18kg\cdot 10.5cm}{8kg+18kg}\\x_p=9.58cm[/latex]
[latex]y_p=\frac{\sum m_i y_i}{\sum m_i}\\y_p=\frac{8kg\cdot 3.5cm+18kg\cdot 3.5cm}{8kg+18kg}\\y_p=3.5cm[/latex]
[latex]z_p=\frac{\sum m_i z_i}{\sum m_i}\\z_p=\frac{8kg\cdot 3.5cm+18kg\cdot 22cm}{8kg+18kg}\\z_p=16.3cm[/latex]
[latex]\underline{\underline{P}=(9.58\underline{\hat{i}}+3.5\underline{\hat{j}}+16.3\underline{\hat{k}})cm}[/latex]
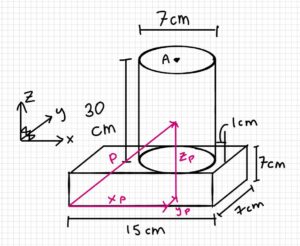
Part d (find the inertia of the person’s leg about point A):
Step 1: Find the MMOI of the foot about f (Iff)
[latex]x_f=0.15m\\z_f=0.07m\\m_f=8kg[/latex]
[latex]I_{ff}=\frac{1}{12}\cdot m\cdot (x^2+z^2)\\I_{ff}=\frac{1}{12}(8kg)(0.15m^2+0.07m^2)\\I_{ff}=0.0183kg\; m^2[/latex]
Step 2: Find the MMOI of the foot about P (IPf)
[latex]d^2=(0.0208m)^2+(0.128m)^2\\I_{pf}=I_{ff}+m_f(d_f)^2\\I_{pf}=0.0182kgm^2+8kg[(0.0208m)^2+(0.128m)^2]\\I_{pf}=0.1527kgm^2[/latex]
Step 3: Find the MMOI of the leg about L (ILL)
[latex]r=0.035m\\h=0.3m\\m_L=18kg\\I_{LL}=\frac{1}{12}\cdot m\cdot (3_r^2+h^2)\\I_{LL}=\frac{1}{12}\cdot 18kg(3(0.035m)^2+(0.3m)^2)\\I_{LL}=0.1405kgm^2[/latex]
Step 4: Find the MMOI of the leg about P (IPL)
[latex]r_{LP}=[(9.58-10.5)\underline{\hat{i}}+(3.5-3.5)\underline{\hat{j}}+(16.3-22)\underline{\hat{k}}]cm\\r_{LP}=(-0.92\underline{\hat{i}}-5.7\underline{\hat{k}})cm\\I_{PL}=I_{LL}+m(d^2)\\I_{PL}=0.1405kgm^2+18kg[(0.0092m)^2+(0.057m)^2]\\I_{PL}=0.2005kgm^2[/latex]
Step 5: Find the MMOI of the entire system about P (IP)
[latex]I_p=I_{PL}+I_{pf}\\I_p=0.1527kgm^2+0.2005kg\\I_p=0.3532kgm^2[/latex]
Step 6: Find the MMOI of the entire system about A (IA)
[latex]A=(10.5\underline{\hat{i}}+3.5\underline{\hat{j}}+37\underline{\hat{k}})cm\\P=(9.58\underline{\hat{i}}+3.5\underline{\hat{j}}+16.3\underline{\hat{k}})cm\\r_{AP}=P-A\\r_{AP}=[(9.58-10.5)\underline{\hat{i}}+(3.5-3.5)\underline{\hat{j}}+(16.3-37)\underline{\hat{k}}]cm\\r_{AP}=(-0.92\underline{\hat{i}}-20.7\underline{\hat{k}})cm[/latex]
[latex]I_A=I_p+m(d^2)\\I_A=0.3532kgm^2+(8kg+18kg)[(0.0092m)^2+(0.207m)^2]\\I_A=1.4695kgm^2\\\underline{I_A=1.47kgm^2}[/latex]
6. Review
It makes sense that the numbers are small, since before the final step, the mass was small, or the distance to the new axis was small.
Example 7.6.2 Inertia, Submitted by Luke McCarvill
1. Problem
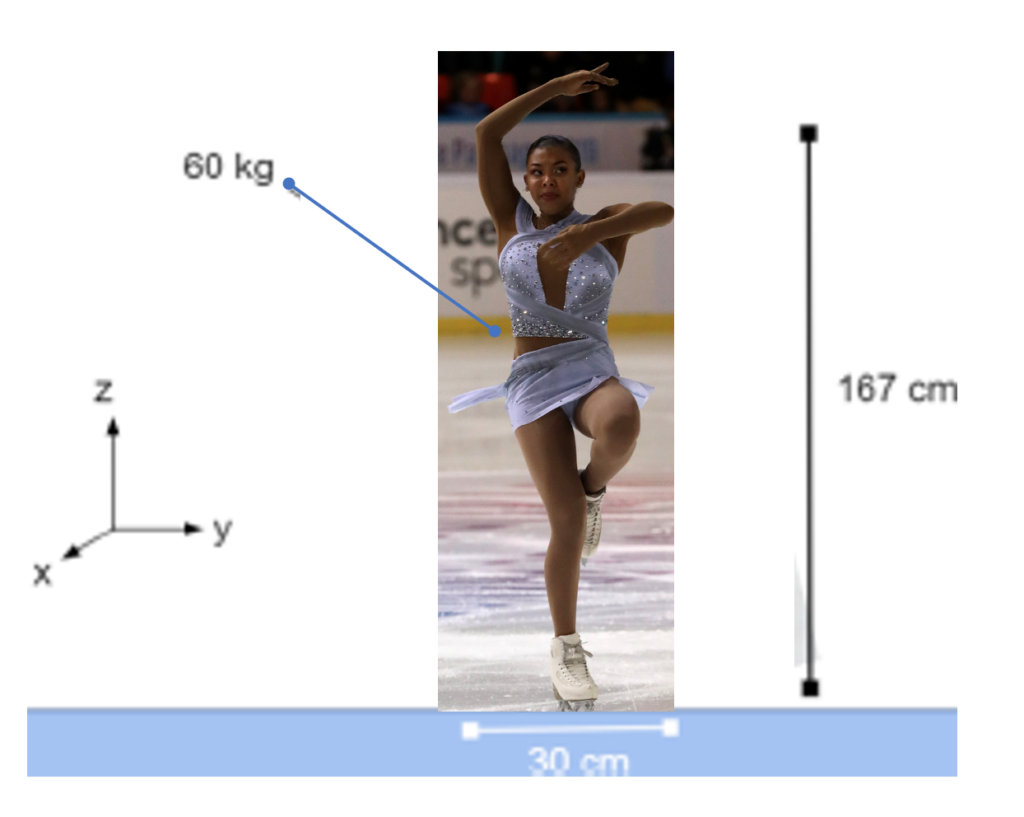
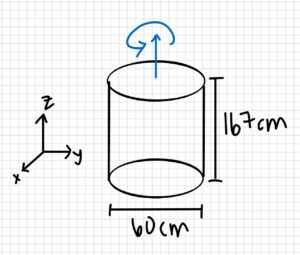
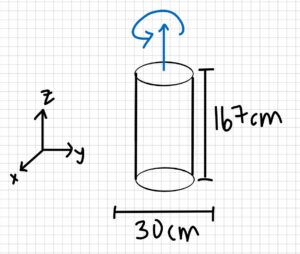
A figure skater with a mass of 60 kg is about to perform a spin about her long axis (z). She is 167 cm tall, and her body can be approximated as a circular cylinder of 30 cm diameter while her limbs are at her side, and a circular cylinder of 60 cm diameter while her arms (and one leg) are outstretched.
a) What should she do in order to generate the highest angular acceleration, assuming she can generate a net torque of 200 Nm? Does lowering her height increase or decrease her angular acceleration?
b) How fast will she be spinning after 0.5 seconds of her maximum vs minimum accelerations, assuming she starts from zero (⍵0 = 0 rad/sec)?
2. Draw
3. Knowns and Unknowns
Knowns:
- m = 60 kg
- ΣM = 200Nm
- h = 167cm
- d1 = 30cm
- d2 = 60cm
- t = 0.5sec
- Izz = ½ mr2
- ΣM = I∝
- ⍵0 = 0rad/sec
Unknowns:
- ∝1 = ?
- ∝2 = ?
- Izz1 = ?
- Izz2 = ?
- ⍵1 = ?
- ⍵2 = ?
4. Approach
I’ll be using MMOI for circular cylinders, as well as the sum of moments/torque equaling MMOI times angular acceleration, as well as acceleration equaling change in velocity over time.
5. Analysis
Part a:
Step 1: Find the inertia when the arms are hugged to the body
Izz1 = 0.5 (60kg) (0.15m)2
Izz1= 0.675 kg m2
Step 2: Find the inertia when the arms are spread out
Izz2 = 0.5(60kg)(0.3m)2
Izz2 = 2.7 kg m2
Step 3: Find the angular acceleration for both cases
ΣM = I∝ ; therefore, ΣM/I = ∝
∝1 = ΣM / Izz1
∝1 = 200 Nm / 0.675 kg m2
∝1 ≈ 296.296 rad/sec2
∝2 = ΣM / Izz2
∝2 = 200Nm/2.7 kg m2
∝2 ≈ 74.074 rad/sec2
The acceleration when the skater had her arms close to her body was about 296 rad/sec2, while that when she had her arms spread out was about 74 rad/sec2. Therefore, having her limbs closer to her body will give her a much higher angular acceleration!
As seen in the equation Izz = ½ m r2, her height is arbitrary; thus, lowering her height would not change the inertia, nor would it change her angular acceleration.
Part b:
∝ = ⍵/t therefore ∝*t = ⍵
⍵1 = 296.296 s-2(0.5s)
⍵1 = 148.148 rad/sec
⍵2 = 74.074 s-2(0.5s)
⍵2 = 37.037 rad/sec
Given that these are in radians per second, let’s convert this to rotations per second to make it more meaningful. To do so, simply divide by 2π since there are 2π radians per rotation. Thus, with her arms in, she can achieve about 23.6 rotations per second after 0.5 seconds of acceleration, compared to about 5.9 rotations per second with her limbs out. This is on par with an Olympian, according to this site.
6. Review
It makes sense that they spin faster when their limbs are hugged to their body; we can try this at home with a swivel chair!
Example 7.6.3: All of Ch 7, Submitted by Victoria Keefe
1. Problem
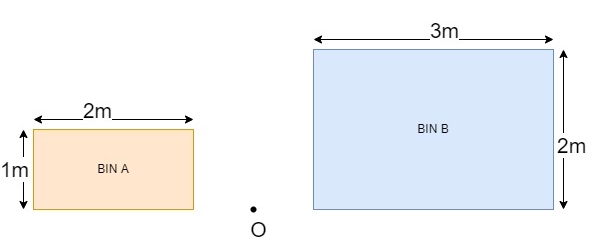
Two rectangular compost containers are tied end to end with a 2 m chain of negligible mass. Container A has a mass of 5 kg with a height of 1 m and a width of 2 m. The container B is of 8kg, height 2m, and width 3m. Consider the point which is the center of the chain as the origin of the coordinate frame to find the center of mass, center of gravity, and centroid of the system and the individual containers.

The real-life scenario of the problem would look similar to the image.
2. Draw
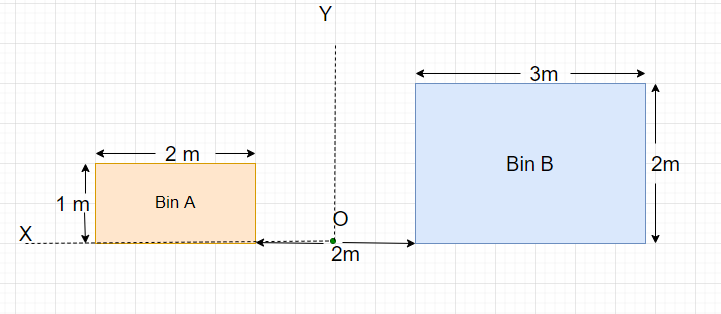
- mA = 5 kg
- mB = 8 kg
- hA = 1 m
- hB = 2 m
- wA = 2m
- wB = 3 m
- d = 2 m
Unknowns:
- [latex]\bar{x_A}[/latex]
- [latex]\bar{x_B}[/latex]
- [latex]\bar{y_a}[/latex]
- [latex]\bar{y_b}[/latex]
- [latex]\bar{x_s}[/latex]
- [latex]\bar{y_s}[/latex]
- [latex]\bar{r_s}[/latex]
Calculate the System centre of mass in y:
[latex]cm_{sy} = \frac {{m_A} \cdot \bar{x}_{ay} +m_B\cdot \bar{x}_{by}} {m_A+m_B}\\ = \frac{5kg \cdot 0.5m +8kg\cdot 1m }{5 kg +8kg}\\ = 0.808m[/latex]
Example 7.6.4: All of Ch 7, Submitted by Deanna Malone
- Problem
A woman doing yoga weighs 65 kg, and her legs are 85 cm long. The combined mass of both her legs is 11.7 kg, one of which is lifted 90 cm above the ground (as in the image below). Her torso contributes to 50% of her mass and is 60 cm long. Her arms are 4.5 kg each, and they are 90 cm from the fingertips to the shoulder. What is her center of gravity in the warrior 3 pose from the origin?

2. Draw
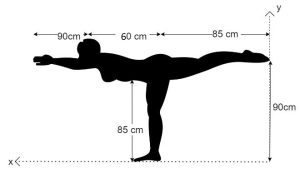
3. Knowns and Unknowns
Knowns:
- m= 65 kg
- mL = 11.7 kg
- mA = 4.5 kg
- mT = 50% of 65 kg
Unknowns:
- [latex]\overrightarrow{r}[/latex], vector from origin to center of gravity
Assumptions
g= 9.81 m/s2
4. Approach
Calculate mass and distance from origin, keeping in mind that the mass distribution is different for legs, torso, and arms, but assuming that the mass is evenly distributed within each of these parts. Use the center of gravity equation.
5. Analysis
Point of mass for leg in air – 11.7 kg at 90 cm up and 42.5 cm left from the origin.
Point mass for leg on ground – 11.7 kg at 42.5 cm up and 90 cm left.
Point mass for torso – 32.5 kg at 90 cm up and 115 cm left.
Point mass for both arms – 9 kg at 90 cm up and 190 cm left.
[latex]\bar{x_m}=\frac{(m_L\cdot0.425m)+(m_L\cdot0.90m)+(m_T\cdot1.15)+(2\cdot m_A\cdot1.90m)}{m}[/latex]
[latex]\bar{x_m} = \frac{(11.7 kg \cdot 0.425 m ) + (11.7 kg \cdot 0.90 m )+(32.5 kg \cdot 1.15 m )+(2 \cdot 4.5 kg \cdot 1.90 m) }{65 kg}[/latex]
[latex]\bar{x_m }=1.08 m[/latex]
[latex]\bar{y_m} = \frac{(m_L\cdot0. 9m)+(m_L\cdot0.425m)+(m_T\cdot0.9)+(2\cdot m_A\cdot0.90m)}{m}[/latex]
[latex]\bar{y_m} = \frac{(11.7 kg \cdot 0.90 m ) + (11.7 kg \cdot 0.425 m )+(32.5 kg \cdot 0.90 m )+(2 \cdot4.5 kg \cdot 0.90 m) }{65 kg}[/latex]
[latex]\bar {y_m} = 0.81 m[/latex]
in vector form, [latex]\overrightarrow{r}=\begin{bmatrix}1.08m\\0.81m \end{bmatrix}[/latex]
6. Review
The answer makes sense because it is close to where the torso is, and it has the most mass. It is a little lower than the torso, which makes sense as this pose would lower the center of gravity.
Example 7.6.5: All of Ch 7, Submitted by Liam Murdock
- Problem
You are the engineer for a tech company, and your role is to design a new extended mount for their new phones. Currently, you are trying to figure out what distance the mount can be from the hand “d”.
You can only use the equation for the midpoint of the rod Izz = (1/12)ml2at your disposal, and the pole weighs 15 N. If a hand is held up the pole at the bottom, it can have a mass moment of inertia of 5 kgm2 before breaking (Iz’z’). Figure out what size the extended mount can be (d).

2. Draw
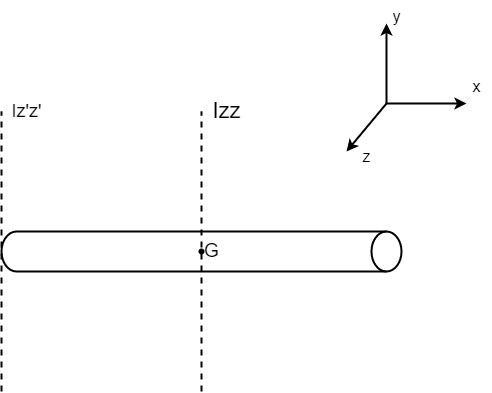
3. Knowns and Unknowns
Knowns:
- Wp =15 N
- g = 9.81 m/s2
- Izz = (1/12)ml2
- Max Iz’z’ =5 kgm2
Unknowns:
- L, length of stick
4. Approach
Newton’s Second Law, Parallel Axis Theorem, Understanding of Mass Moment of Inertia
5. Analysis
[latex]m = \frac{w_p}{g}[/latex]
[latex]m = \frac{15N} {9.81 \: m/s^2}[/latex]
[latex]m = 1.529\: kg[/latex]
[latex]I_g =\frac{1}{12}\:md^2[/latex]
[latex]Iz'z' = I_g + ml^2[/latex]
[latex]Iz'z' = \frac{1}{12}\:md^2+m\times \left(\frac{1}{2}d\right) ^2[/latex]
thus,
[latex]5kgm^2 = \left (\frac{1}{12}\times (1.529kg)\times d^2 \right)+\left(1.529kg\: \times \frac{1}{4}d^2\right)[/latex]
[latex]d =3.13 m[/latex]
In conclusion, the maximum size the pole can be is 3.13 m without the device breaking.
6. Review
Applying the derived value of d in
[latex]Iz'z' = \frac{1}{3}md^2[/latex]
[latex]Iz'z' =\frac{1}{3}\times (1.529kg)\times(3.13m)^2[/latex]
[latex]Iz'z' = 4.99999kgm^2 =5.0kgm^2[/latex]
According to the equation, the max distance of 3.13 m does make sense
Example 7.6.6: Center of Mass, Submitted by Dhruvil Kanani
1. Problem

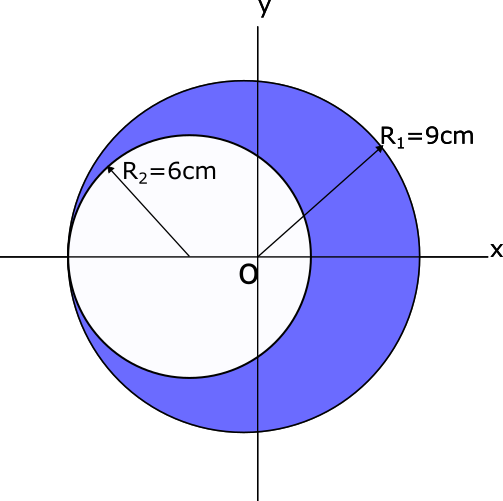
3. Knowns and Unknowns
Knowns:
- Mass of Initial disc: m1 = 50.87kg
- Radius of larger disc: r1 = 18cm/2 = 9cm
- Radius of cut: r2 = 6cm
Unknowns:
- Mass of crescent: m2
- Center of mass of crescent: CMc
4. Approach
Use the mass and radius of the larger disc to find the density of the material. Calculate the area of the crescent
Use the area and density to find the mass of the crescent.
Find the center of mass of the smaller circle.
Use the center of mass of each circle and the mass of each circle to determine the center of mass of the crescent.
5. Analysis
Density of materials:
[latex]\rho = \frac{m_1}{2\pi \cdot r_1 ^2} \\ \rho = \frac{50.87kg}{2\pi \cdot 9^2} \\ \rho = 0.1kg/cm^2[/latex]
Area of crescent Ac :
[latex]A_c = 2\pi \cdot (r_1 ^2 - r_2 ^2) cm^2 \\ A_c = 2\pi \cdot (9^2 - 6^2) cm^2 \\ A_c = 90\pi cm^2[/latex]
Mass of crescent:
[latex]m_2 = \rho \cdot A_c \\ m_2 = 0.1kg/cm^2 \cdot 90\pi cm^2 \\ m_2 = 9\pi kg \approx 28.27kg[/latex]
Center of mass of the cut circle:
Since the edge of the cut circle lines incident to the larger circle, the radius of the cut can be subtracted from the radius of the full disc to find the center of mass of the cut, CMcut
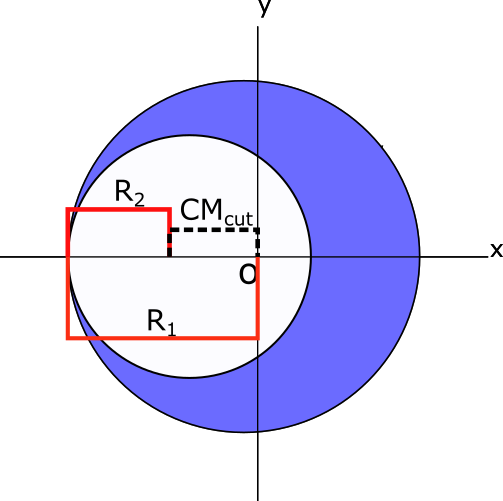
[latex]CM_{cut x} = R_1 - R_2 \\ CM_{cut x} = 9cm - 6cm \\ CM_{cut x} = 3cm[/latex]
CMcut x is 3cm in the negative x direction.
CMcut y is equal to 0 as the center of mass of both the disc and the cut is zero in the y-direction.
The center of mass of the full disc is at [0cm, 0cm] as it’s centred at the origin.
Center of mass of the crescent:
The center of mass of the full circle (CMfull) is [0cm, 0cm] and its mass m1 = 50.87kg.
The center of mass of the cut (CMcut) is [-3cm, 0cm], and its mass (mcut) is the mass of the crescent minus the mass of the full circle: 28.27kg – 50.87kg = -22.6kg.
The center of mass of the crescent CMc is:
[latex]CM_{cx} = \frac{(CM_{full x} \cdot m_1) + (CM_{cut x} \cdot m_{cut})}{m_2}[/latex]
[latex]CM_{cx} = \frac{(0cm \cdot 50.87kg) + (-3cm \cdot -22.6kg)}{28.27kg}[/latex]
[latex]CM_{cx} = 2.4cm[/latex]
Both the center of mass of the full circle and the cut in the y-direction are 0cm, giving the center of mass of the crescent in the y-direction also 0cm.
The complete center of mass of the crescent is therefore:
CMc = [2.4cm, 0cm]
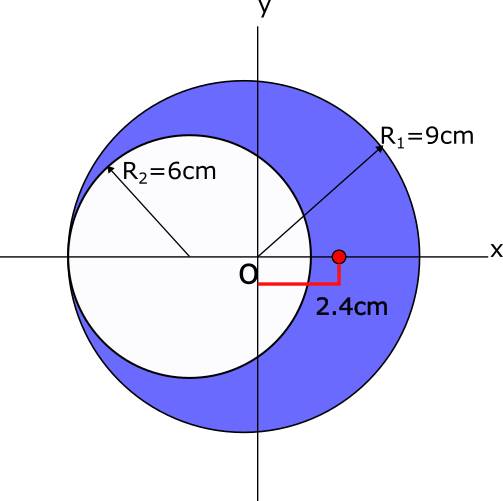
6. Review:
The center of mass of the crescent leans to the side with more mass, as one would expect. The mass and center of mass found are both in the expected units with a reasonable magnitude.
Example 7.6.7: Mass moment of inertia, Submitted by Michael Oppong-Ampomah
1. Problem
An empty tissue paper roll rolls down an angled floor. If the tissue paper roll weighs 2 lbs, has and inner radius 0.9 inches, total diameter 2 inches, and a length of 12 inches, then calculate the mass moment of inertia of the roll.
2. Draw
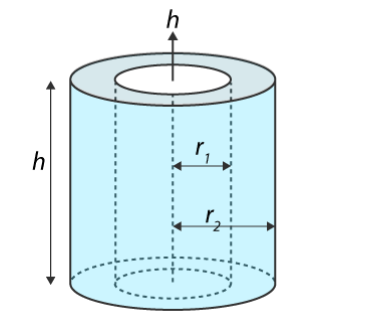
3. Knowns and Unknowns
Knowns:
w = 2 lbs
Inner radius r1 = 0.9 in
Outer radius r2 = 1 in
h=12 in
Unknowns:
Mass moment of inertia
4. Approach
Finding the mass of the roll, identifying the axis of rotation, and applying the corresponding mass moment of inertia of the cylinder.
[latex]I_{x}= \frac{1}{2} m(r_{1}^2 + r_{2}^2)[/latex]
[latex]I_{y}= I_{z}= \frac{1}{12} m[3(r_{1}^2 + r_{2}^2)+h^2][/latex]
5. Analysis
weight of the roll = 2 lb
mass of the roll, [latex]m = \frac{2 lb}{32.2 ft/s^2} = 0.062 lb[/latex]
Since we used constant of gravity with a unit of [latex]ft/ s^2[/latex] it is important to convert other values from inches to ft.
[latex]0.9 in = \frac{0.9}{12}=0.075 ft[/latex]
[latex]1 in =\frac{1}{12} = 0.083 ft[/latex]
[latex]12 in = 1 ft[/latex]
now, [latex]I_{x}= \frac{1}{2} m(r_{1}^2 + r_{2}^2)[/latex]
[latex]I_{x} = \frac{1}{2} 0.062(0.075^2 + 0.083^2) = 0.00039 \quad lb ft^2[/latex]
[latex]I_{y}= I_{z}= \frac{1}{12} m[3(r_{1}^2 + r_{2}^2)+h^2][/latex]
[latex]I_{y}= I_{z}= \frac{1}{12} 0.062[3(0.075^2 + 0.083^2)+1^2] =0.0054 \quad lb ft^2[/latex]
6. Review
Although the weight of an empty paper roll is exaggerated for easier calculation, the answers make sense. The value of Iy is higher than Ix, which means more force will be needed for rotation in that axis. From this, it is important to note that the roll will rotate along the x-axis. Also note that weight is converted to mass, and units must be the same.

