1. Problem

A flower cart at a local garden center is being pushed with a force of 500N at joint G. Its back wheels (A) are locked, so it is not moving. There is 1 meter of space between each of the four shelves in height, and each shelf is four meters long.

a) Calculate the reaction forces of the locked wheels and the unlocked wheels.

b) Calculate the load carried by F_CG, and whether it is in tension or compression

Which method did you use, joints or sections? Which is faster for the style of questions? How would your strategy change if you were calculating the load in each member?

2. Draw

Sketch:

Free-body Diagram:

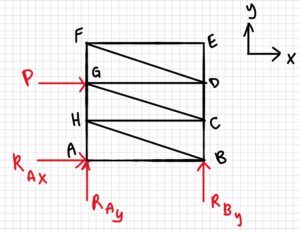
3. Knowns and Unknowns

Knowns:

• P = 500 N
• Width = 4 m
• Total height = 3 m

Unknowns:

• R_Ax
• R_Ay
• R_By
• F_CG

4. Approach

Part a: Determine reaction forces using equilibrium equations

Part b: Calculate F_CG using the method of sections. Make a cut, then solve internal forces using equilibrium equations

5. Analysis

Part a:

Solving for R_Ax:

$$\sum F_x=0=P+R_{Ax}\\R_{Ax}=-P\\R_{Ax}=-500N$$

Solving for R_By:

$$\sum M_A=0=(r_{BA}\cdot R_{By})-(r_{GA}\cdot P)\\r_{BA}\cdot R_{By}=r_{GA}\cdot P\\R_{By}=\frac{r_{GA}\cdot P}{r_{BA}}\\R_{By}=\frac{2m\cdot 500N}{4m}\\R_{By}=250N$$

Solving for R_Ay:

$$\sum F_y=0=R_{By}+R_{Ay}\\R_{Ay}=-R_{By}\\R_{Ay}=-250N$$

The answers we got that were negative numbers mean that the direction of the vector is drawn wrong on our original diagram (in reference to our coordinate frame). This makes sense as R_Ay and R_By are the only external forces in the y direction, so they have to cancel each other for the equilibrium equations to be true (Same for the vectors in the x direction.) Therefore, one of them should have a negative direction. We will leave this answer as is for now, but the next time we draw the system, we will change the direction of the arrow.

$$ \underline{R_{Ax}=-500N,\; R_{Ay}=-250N, \; R_{By}=250N}$$

Part b:

Firstly, we redraw the diagram, changing the direction of the R_Ay and R_Ax. Then, since we are using the method of sections, we make a cut so that the member F_CG (the one we want to find) is cut.

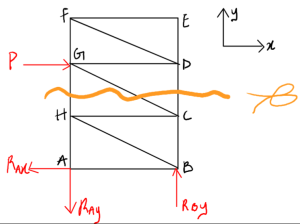
Now we redraw, choosing one of the pieces from the cut. Here the top half is chosen, but you could also choose the bottom half and get the right answer. The only reason the top half was chosen here is because there are fewer external forces to consider for the top.

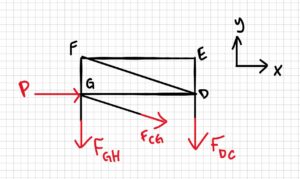
Solve for the member we are looking for:

 $$\sum F_x=0=P+\frac{4}{\sqrt{17}}F_{CG}\\\frac{4}{\sqrt{17}}F_{CG}=-P\\F_{CG}=-P(\frac{\sqrt{17}}{4})\\F_{CG}=-500N(\frac{\sqrt{17}}{4})\\F_{CG}=-515.388N$$

Again, the number we get is negative. The way we drew F_CG originally was as if the member was in tension. The negative number just means that it is actually compression, not tension.

$$ \underline{F_{CG}=515 \text{N (Compression)}}$$

Part C:

For part b, I used the method of sections, as it would be the fastest method. The method of joints would require the lower joints to be solved first, which would be a much slower process, whereas with this method, a simple cut can be made and the member ‘s load can be quickly solved using equilibrium equations. Had the question asked for all member loads to be solved, however, the method of joints would have been the faster approach.

6. Review

Part a:

R_Ax is equal and opposite to P so we know it is correct, and the value of R_By should also be correct as its moment about A (250 * 4m = 1000 Nm), is equal and opposite to the moment of P about A, (500 N * 2 m = 1000 Nm). as R_Ay is equal and opposite to R_By it is also correct.

Part b:

The x component of the calculated value of F_CG is equal in magnitude to P (see equation below), and it is the only cut member acting in the x direction. Therefore, it must be correct.

$$\frac{4}{\sqrt{17}}(515 N)=500 N$$

Part C:

The method of sections allows you to solve a very specific area of the system’s internal forces (the members that are cut), whereas the method of joints usually requires you to solve most, if not all, of the internal forces of the system. Therefore, the method of sections is the most efficient for finding the internal forces of specific parts of the system, whereas the method of joints is more efficient for solving the whole system.

1. Problem

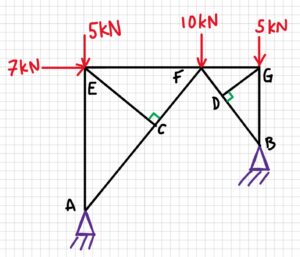
2. Draw

Free-body diagram:

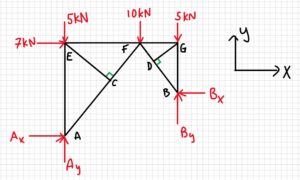
3. Knowns and Unknowns

Knowns:

• All of the known values do not mean anything – we only need to know where the forces exist

Unknown:

• Which members are zero-force

4. Approach

Look at each joint and determine how many forces are in each direction. If there is only one force in a direction, that member is zero-force.

5. Analysis

Part a:

Let’s start with joint C. If we think of the forces acting in the x and y directions as shown below by the coordinate frame, we see that there are two forces acting in the y direction, and only one in the x direction. Therefore, assuming the joint is in static equilibrium, member CE is a zero-force.

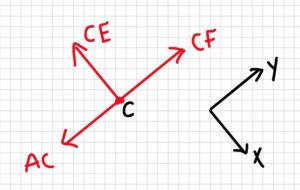
If we do the same type of analysis for the other joints and remove the zero-force members, the structure now looks like this:

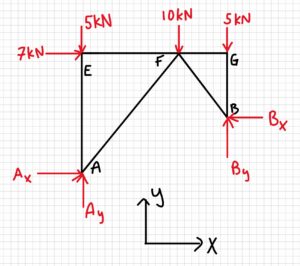
After one more analysis of the joints, we find one more zero-force member, as shown below.

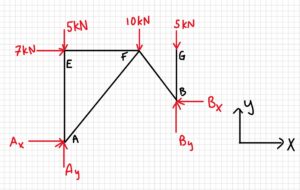
Answer: CE, DG, and FG are zero-force members.

Part b:

Zero-force members exist to provide stability to the truss, to keep the shape rigid.

6. Review

Although the new truss (without zero-force members) looks strange, there are no joints where there’s only one force in one direction, therefore there are no more zero-force members.

1. Problem 

2. Draw

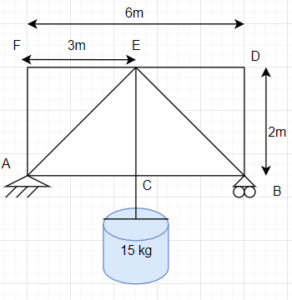
3. Knowns and Unknowns

Knowns:

• F_g = 15 kg . 9.81 m/s² = 147.15 N
• r_AF = r_BD = r_CE =2 m
• r_DF = r_AB = 6 m

Unknowns:

• R_Ax
• R_Ay
• R_By
• F_EF
• F_ED
• F_BD
• F_BE
• F_CE
• F_AE
• F_AC
• F_BC
• F_AF

4. Approach 

First, use the equilibrium equations to find the reaction forces. Apply these reaction forces in the method of joints to find the force of each member.

5. Analysis 

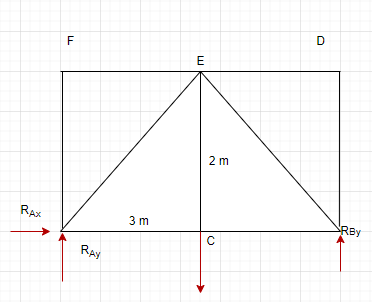
a. Calculating the reaction forces using the equilibrium equations and the diagram.

$$\sum F_x=0=R_{Ax}\\R_{Ax}=0N$$

Solving for R_By:

$$\sum M_A=0= -(r_{AC}\cdot F_g)+(r_{AB}\cdot R_{By})\\r_{AB}\cdot R_{By}=r_{AC}\cdot  F_g $$

$$R_{By}=\frac{r_{AC}\cdot F_g}{r_{AB}}\\R_{By}=\frac{3m\cdot 147.15 N}{6m} $$

$$R_{By}=73.575 N$$

Solving for R_Ay:

$$\sum F_y=0=R_{By}+R_{Ay} -F_g\\R_{Ay}=F_g-R_{By}\\R_{By}=73.575N$$

b. F_AF, F _EF, F_DE, F_BD are zero force members because for joints F and D, there are only 2 members each, and there is no external load.

Finding the angle between AC and AE:

tan θ = r_CE/r_AC

therefore, θ = 33.7 °

Analyzing joint A:

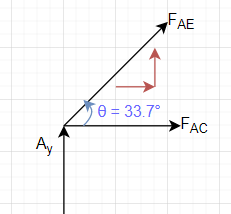
$$\sum F_y=0 = R_{Ay}+ F_{AE}\cdot sin 33.7 \\ =\frac{-73.575 N}{sin 33.7} $$

$$ F_{AE} = -132.6 N $$

$$\sum F_x=0 = F_{AC} + F_{AE} cos 33.7\\ F_{AC}=132.6N\cdot \cos {33.7}$$

$$ F_{AC} = 110.32 N $$

Analyzing Joint C:

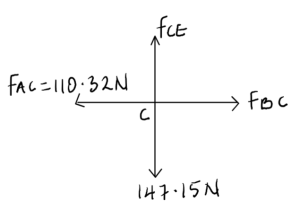
From the FBD,

F_AC= F_BC = 110.32 N

Also, F_g  =F_CE = 147.15 N

Analyzing Joint B

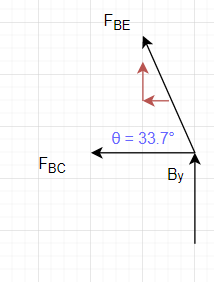
$$\sum F_y=0 = R_{By} +F_{BE}\cdot sin 33.7  $$

$$ F_{BE} = -132.6 N $$

$$\sum F_x=0 = F_{BC} -F_{BE} cos 33.7\\ F_{BC}=132.6N\cdot \cos {33.7}$$

$$ F_{BC} = 110.32 N $$

c.

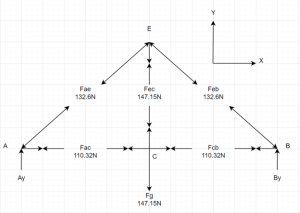
6. Review 

The answers make sense because F_CEis in tension as imagined due to the weight of the bucket. Members AC and BC are under reaction forces, are equally under tension, and members AE and BE are balanced by compression. The identified zero-force members also make sense due to the rules being met.

1. Problem

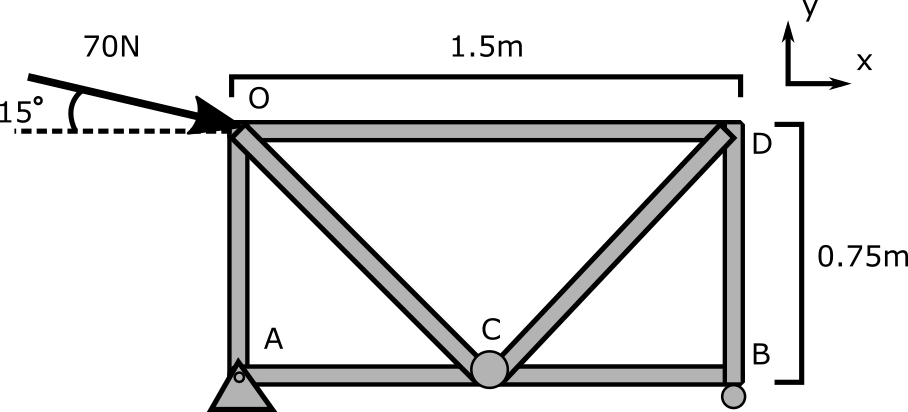
2. Draw

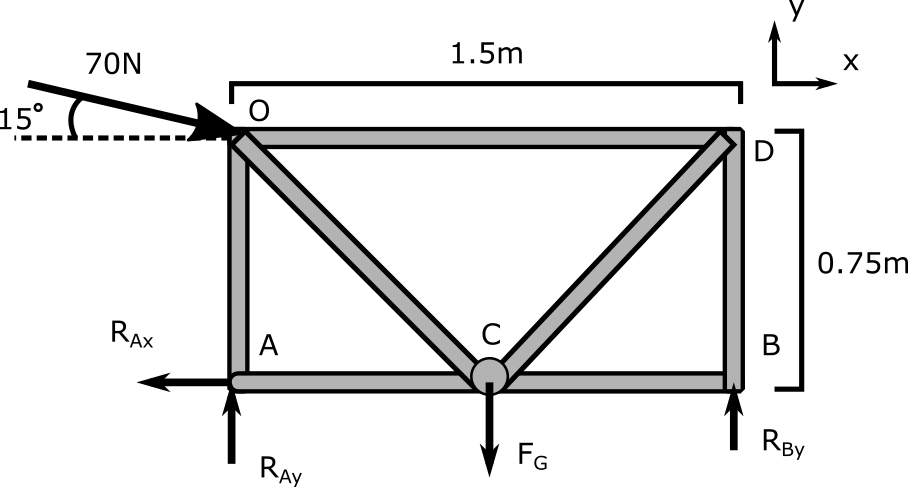
3. Knowns and Unknowns

Knowns:

• [latex]P = 70\,N[/latex]
• [latex]\sum M = 0[/latex]
• [latex]h = 0.75\,m[/latex]
• [latex]\theta_p = 15^\circ[/latex]
• [latex]d_{\text{rod}} = 2\,\text{cm (diameter)}[/latex]
• [latex]\sum F = 0[/latex]
• [latex]\rho = 8.00\,\text{g/cm}^3[/latex]
• [latex]V_{\text{cylinder}} = \pi r^2 h[/latex]

Unknowns:

• [latex]m_{\text{tot}} = \, ?[/latex]
• [latex]P_x = \, ?[/latex]
• [latex]P_y = \, ?[/latex]
• [latex]R_{Ax} = \, ?[/latex]
• [latex]R_{Ay} = \, ?[/latex]
• [latex]R_{By} = \, ?[/latex]
• [latex]F_g = \, ?[/latex]

4. Approach

Use trigonometry and equilibrium equations, as well as the method of joints, to calculate unknowns

5. Analysis

Finding total mass:

There are four 75cm rods, two rods that are [latex]75\sqrt{2}[/latex]cm, and one rod that is 1.5m long, all of which have a diameter of 2cm. The total mass is therefore $$ 8g/cm^3 \cdot ((4 \pi \cdot (1cm)^2\cdot (75cm) + 2\pi\cdot (1cm)^2 \cdot \\ (75 \sqrt(2)cm) + \pi  (1cm)^2 \cdot (150cm)) \\ \approx 16,641g = 16.641kg = m_{tot}$$

F_g can then be found using $$ F_g = g \cdot m_{tot} = -9.81m/s^2 \cdot 16.641kg \approx -163.25N$$

The sum of forces and moments can now be used to determine reaction forces

$$ \sum F_x = P_x – R_{Ax} \\ R_{Ax} = P \cdot cos(\theta) = 70N cos(15^\circ) \\ R_{Ax} \approx 67.6N$$

$$\sum F_y = -F_g – P_y + R_{Ay} + R_{By} = 0$$

With two unknowns, sum of moments must be considered. Summing moments around point A finds:

$$ \sum M_A = 0 = -(0.75m \cdot Pcos(\theta)) – (0.75m \cdot F_g) + (1.5m \cdot R_{By}) $$

$$ \sum M_A = 0 = -(0.75m \cdot 70N cos(15^\circ)) – (0.75m \cdot 163.25N) + (1.5m \cdot R_{By})$$

$$ R_{By} \approx 115.43N$$

Sum of Forces in Y can now be used to find R_Ay

$$ F_y = -F_g – P_y + R_{Ay} +R_{By} = 0$$

$$ R_{Ay} \approx 65.94N $$

The method of joints can now be used to determine if any zero-force members exist in the shopping cart.

Looking at Point A, it can be found that [latex]F_{AO} = 65.94\,N[/latex] in compression and [latex]F_{AC} = 67.6\,N[/latex] in tension. Continuing through each joint, it can be found that member CB is a zero-force member as point B only has one component in the X direction, which, in a static system, implies that the force must be zero.

6. Review

Given the high weight of the cart creating a large F_g and the applied force of 70N, the reaction forces found and the internal forces all seem to be of appropriate magnitude and direction.

1. Problem

You are designing a shelf for a friend, and it can be analyzed as a truss shown below. If you know the forces in the member CD can take a tensile force of 25 N, and GH can take a compressive force of 15 N before breaking. If w = 10 cm and h = 20 cm, what mass can be supported if it is situated exactly on point E?

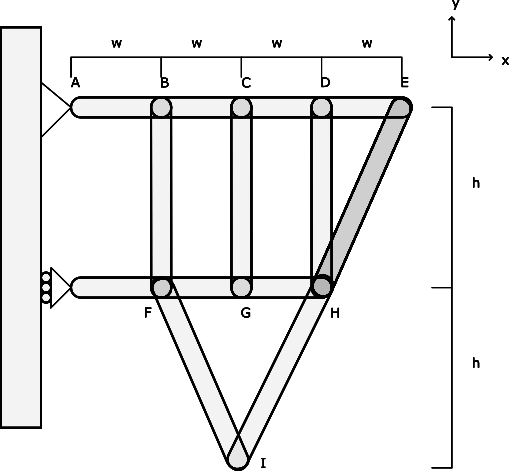
2. Sketch
Draw a free-body diagram of the truss with a slice through CD, GH, and IH.

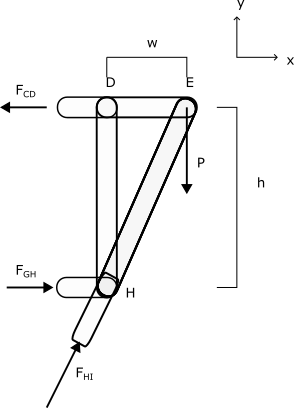
3. Knowns and Unknowns

Knowns:

• w = 0.1 m
• h = 0.2 m
• F_CD = -25 N
• F_GH = 15 N

Unknowns:

• F_HI =?
• d_HI = ?
• P =?
• m = ?

4. Approach
Use the method of sections to show internal forces and analyze as a rigid body.

5. Analysis
First, the distance d_HI can be found:
$$ d_{HI} = \sqrt{(0.1 m)^2 + (0.2 m)^2} \\ d_{HI} = 0.2236 m$$
This value can be used to find the equivalents to cosθ and sinθ:
$$ \cos{\theta} = \frac{0.1 m}{0.2236 m} \\ \sin{\theta} = \frac{0.2 m}{0.2236 m} $$
The sum of forces in the X direction can be used to determine the value of F_HI:
$$ \sum F_x = 0 = -F_{CD} + F_{GH} + F_{HI} \cdot \cos{\theta} \\ F_{HI} = \frac{(F_{CD} – F_{GH})}{\cos{\theta}} \\ F_{HI} = \frac{0.2236 m}{0.1 m} \cdot (25 N – 15 N) \\ F_{HI} = 22.36N$$
The sum of forces in the Y direction can now be used to determine the value of P:
$$ \sum F_y = 0 = -P + F_{HI} \cdot \sin{\theta} \\ P = F_{HI} \cdot \sin{\theta} \\ P = (22.36 N) \cdot \frac{0.2 m}{0.2236 m} \\ P = 20 N$$
The mass can now be simply found by dividing the force by gravity:
$$ P = mg \\ m = \frac{P}{g} \\ m = \frac{20 N}{9.81 \frac{m}{s^2}} \\ m = 2.04 kg$$

6. Review
A brief review of this question is the sign and magnitude of the result. The force generated by the mass pushes downwards with gravity, which is expected. The magnitude of the mass, while defining this shelf as one that is particularly flimsy, is a reasonable mass.