Chapter 2: Particles
2.4. Examples
Here are examples from Chapter 2 to help you understand these concepts better. These were taken from the real world and supplied by FSDE students in Summer 2021. If you’d like to submit your own examples, please send them to the author eosgood@upei.ca.
Example 2.4.1: Equilibrium Equation and Components of Vectors, Submitted by Analiya Benny
- Problem
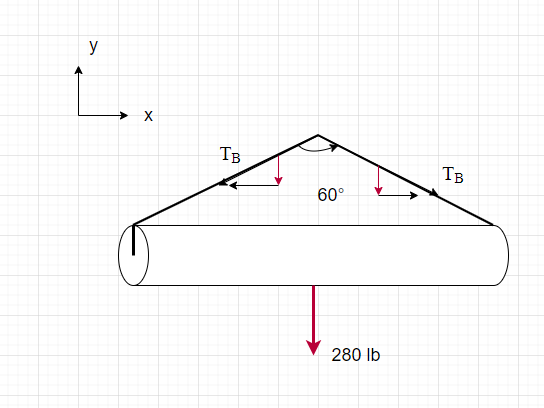
A 280 lb Pipe is being lifted by a crane as shown in the figure. Find the magnitude of the tension on the cables, given that the forces on the cables are equal.
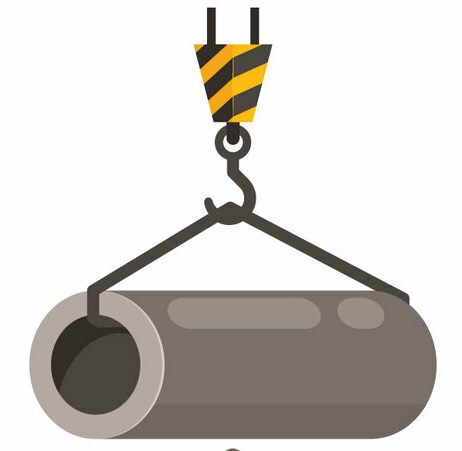
https://publicdomainvectors.org/en/free-clipart/Crane-with-a-pipeai/86375.html
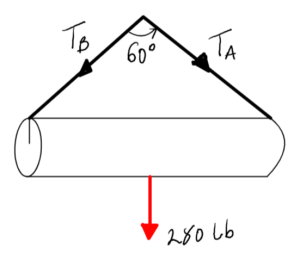
2. Draw
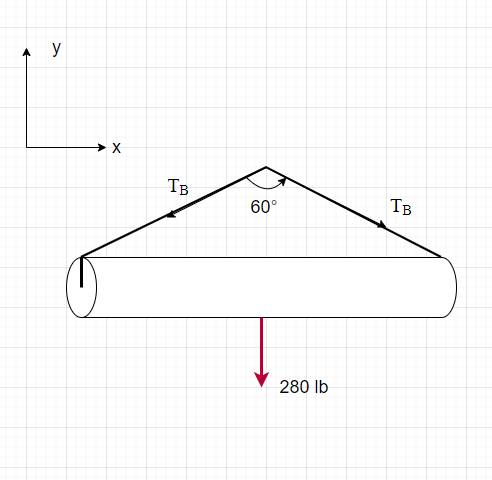
3. Knowns and Unknowns
Knowns:
- F = 280 lb
- θ = 60°
Unknown:
- [latex]\overrightarrow{T_{B}}[/latex]
- [latex]\overrightarrow{T_{A}}[/latex]
4. Approach
Applying the equilibrium equation and componentization of vectors to find [latex]T_{B}[/latex] and [latex]T_{A}[/latex].
Note: [latex]T_{B}[/latex] = [latex]T_{A}[/latex]
5. Analysis
Components of [latex]T_{B}[/latex]
[latex]T_{By} = T_{B} \sin {60}[/latex]
and, [latex]T_{Bx} = T_{B}\cos {60}[/latex]
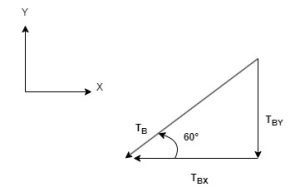
Equilibrium equation in the y direction
[latex]\sum F_{y}= -T_{By} -T_{By}-280 lb = 0 \\ T_{By} = \dfrac{-280 lb}{2} = -140 lb[/latex]
Note that the -ve sign here means that the direction of vector TB is opposite to that drawn in the FBD diagram. So now the FBD is as given below:

now, [latex]T_{B} \sin {60} = 140 lb[/latex]
[latex]T_{B} = \dfrac{140 lb}{\sin{60}}[/latex]
Thus, [latex]T_{B} = T_{A} = 161.66 lb[/latex]
The magnitude of the tension carried by each of the cables is 161.66 lb.
6. Review
The results show that the x component does no essential contribution towards carrying the weight of the pipe because the sum of forces in the x direction just cancels out and equals 0lb.
[latex]\sum F_{x}= -T_{Bx} +T_{Bx}= 0[/latex]
Example 2.4.2: Equilibrium Equation, Submitted by Kylian Duplan
1. Problem
Desmond (80kg) is hanging for his life in a well, on a horizontal pole that is between two brick walls that displace 1200N of force each upwards along the pole. There is also a single brick positioned 2m away from the first wall. If Desmond is hanging 3m away from the second wall, and is to catch a backpack falling above him, what mass should the backpack be to break the pole, causing Desmond to fall into the well? What is the mass of the single brick? [g=9.81m/s^2]
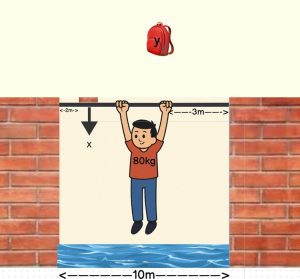
2. Draw
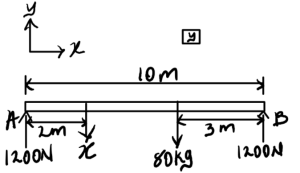
3. Knowns and Unknowns
Knowns:
- Desmond’s mass = 80kg
- Mass of bag caught = (y)kg
- Weight of Desmond + bag, W = 9.81(80 + y)
- Weight of the block = x
- Wall A = First wall
- Wall B = Second wall
- g = 9.81m/s2
Unknowns:
- x
- y
4. Approach
Apply equilibrium equations and solve simultaneously to find x and y
5. Analysis
Taking moment about wall B,
Summing up vertical forces
In kilograms; (Divide by 9.81m/s2)
6. Review
The block would need to weigh 97.86 kg at 2m from Wall A, and Desmond should catch the bag weighing 6.81kg while he hangs 7m from Wall A.
Example 2.4.3: Equilibrium Equation, Submitted Anonymously
1. Problem
A military M35 truck is lifted using a helicopter hover lift and cables whose upper strings are slightly shorter than the lower strings. The shorter-upper strings create an angle of 40 degrees to the top of the truck, and the longer-lower strings create an angle of 60 degrees to the top of the truck. If the truck has a mass of 5000 kg and is evenly distributed, determine:
a. Draw Free Body Diagram at point A, B, and C.
b. what are the tension on each string?

https://garystockbridge617.getarchive.net/media/the-ch-53k-king-stallion-lifts-a-joint-light-tactical-4c867f
2. Draw
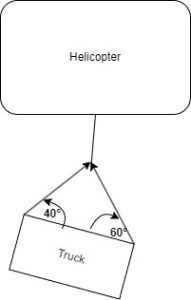
Free Body Diagram:
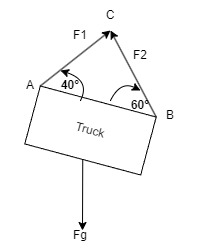
3. Knowns and Unknowns
Knowns:
- m=5000 kg
- ∠A = 40°
- ∠B = 60°
Unknowns:
- F1
- F2
4. Approach
Considering the load is evenly distributed, the upper pair of string have equal lengths, and so does the lower pair, FBD can be drawn for each points. Use equilibrium equations for x and y direction to find tension on each string.
5. Analysis
Weight,[latex]w =m\times g= 5000 kg\times 9.81= 49050 N[/latex]
Point A
[latex]\begin{equation} \sum{F_{y} = F_{1} \sin{40} -\dfrac{w}{4}} \end {equation}[/latex]
[latex]\begin{equation} F_{1} = \dfrac{w}{4\times \sin{40}} = \dfrac{49050}{4\times 0.643} \end{equation}[/latex]
[latex]F_{1} = 19070.76 N[/latex]
Point B
[latex]\begin{equation} \sum{F_{y} = F_{2} \sin{60} -\dfrac{w}{4}} \end {equation}[/latex]
[latex]\begin{equation} F_{2} = \dfrac{w}{4\times \sin{60}} \end{equation}[/latex]
[latex]F_{2} = 14159.51 N[/latex]
Point C
[latex]F_{T} =F_{1}\sin{40} +F_{2}\sin{60}[/latex]
[latex]\begin{equation} \quad\quad = (19070.76\times 0.643) +(14159.51\times 0.866)\end{equation}[/latex]
[latex]F_{T} = 24524.63 N[/latex]
Thus both the upper strings are at a tension of 19070.76 N and lower strings are at a tension of 14159.51 N.
6. Review
Note that in this problem the vehicle’s weight was evenly distributed which is convenient in symmetrical situations like this. The tension on the strings can be verified as follows.
[latex]2F_{T} = m\times g[/latex]
Example 2.4.4: Equilibrium Equation, Submitted by Analiya Benny
1. Problem
A child with a mass of 20kg is sitting on a swing with both strings 4 m long.
a. Draw the free-body diagram.
b. Calculate the tension of the strings.
c. What happens to the tension of the strings when string A is 3 m and string B is 4 m? Explain with a free-body diagram.

Image 1: A real-life demonstration of the situation in the question.
2. Draw
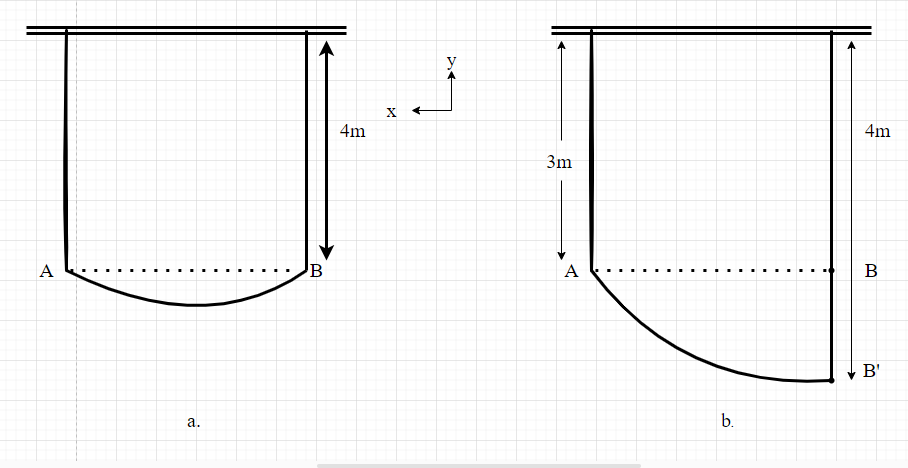
3. Knowns and Unknowns
Knowns:
- [latex]M= 20kg[/latex]
- [latex]g = 9.81 m/s^2[/latex]
Unknowns:
- FA
- FB
4. Approach
Analyzing the dimensions of the situation and applying the equilibrium equation.
5. Analysis
[latex]w = m \times g = 20 kg \times 9.81= 196.2 N [/latex]
b. When the length of the strings is equal, the weight on point A is equal to the weight on point B. FA = FB
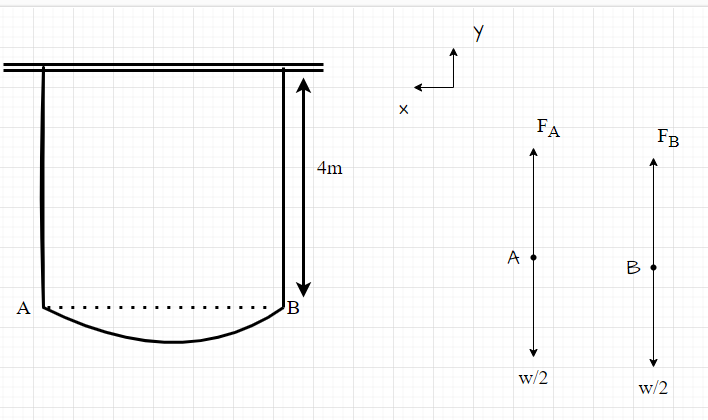
No Force in the x-direction
[latex]\sum F_y = 0 \\ F_A + F_B = 196.2 \, \text{N} \\ F_B + F_B = 196.2 \\ 2F_B = 196.2 \\ F_B = 98.1 \, \text{N} \\ \text{Tension in each string is } 98.1 \, \text{N}[/latex]
c. When one chain of the swing is longer, the tension on the chains varies such that [latex]w_{B}>w_{A}[/latex]; in turn, chain B will experience more tension than chain A. To solve for tension in the chains, we would require more information about the distribution of the weights on points A and B.
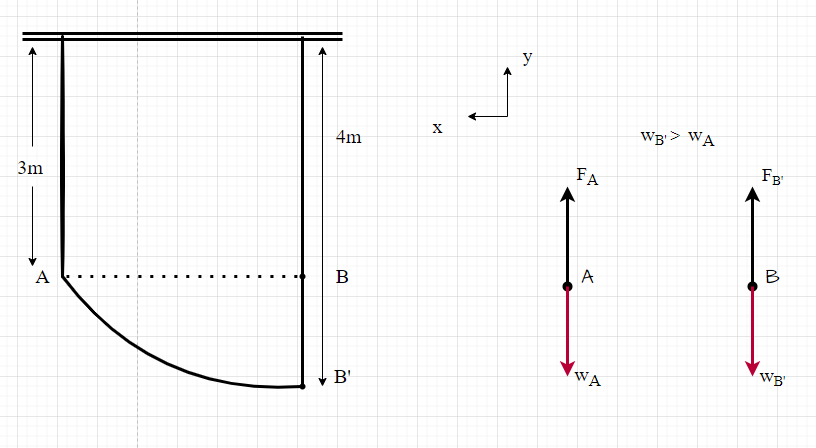
6. Review
In questions involving free-body diagrams, it is convenient to have perfectly symmetrical situations. However, when faced with non-symmetrical or distributed loads, different techniques need to be applied, which will be explained in the following chapters.

