Main Body
10 PHOTONS GET REFRACTED
p. 24
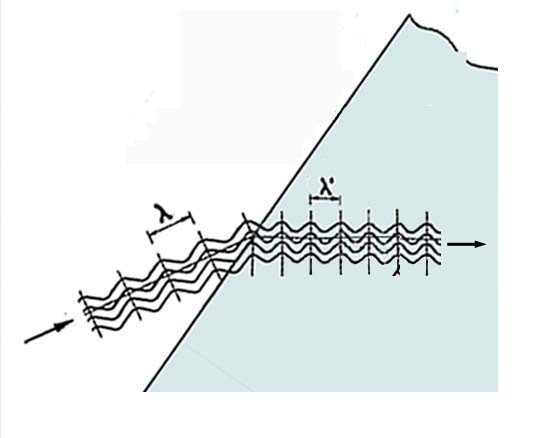
Of particular value is what happens when photons enter a denser transparent medium at an angle. For the briefest of moments, “drag” slows down the first portion of the wave while the remainder continues normally. This changes the photons’ direction of travel inside the new medium.
p. 25
How much their direction is changed depends on the ratio of their speeds in the two media.
To determine the bending, it is not necessary to calculate those speeds The ratio of their refractive indexes (see page 5) will do. The refractive index for various materials is listed in tables available from many sources:

The following math illustrates that these matters are simple trigonometry:
e.g. For air n = 1; for water n = 1.33; for crown glass n = 1.52.In this example, if the medium on the left is air, the denser medium is crown glass, and the angle of incidence on the glass, θ, equals 60 degrees:
sin of the refracted angle Ω =
(nair / nglass) x sin incident angle θ
sin Ω = ( 1 / 1.52) x sin 60o
= 0.66 x 0.87= 0.57 So the refracted angle Ω = 35o
These calculations are the same when photons leave a denser material.
In the above example, the glass surfaces are parallel. Therefore the incident and exit angles are reversed, and the photons leave in the same direction at which they entered – albeit laterally displaced.
p. 26
Higher frequency photons slow more in denser media than low frequency photons. (The refractive index, n of most substances increases with frequency.)
Consequently, on entering a higher refractive index medium, “violet” photons change direction more than lower frequency “red” photons.

(N.B. This is opposite to what happens when photons are diffracted – page 10.)
Refraction sorts photons into slightly different directions depending on their frequency. This is why white light gets spread into a rainbow by prisms and water droplets.
As the photons leave, note how the internal angular differences restore the original direction of each wavelength, though they are now laterally displaced according to wavelength as well as laterally displaced from their original path.
p.27
Colors from diffraction can be used to produce some novel lighting effects. Yet the effect can also result in nuisance colors fringes (chromatic aberration) in some lighting applications.
The above example used a prism with parallel entrance and exit surfaces. If the exit surface had a slightly steeper angle, the various frequency photons could arrive at the same point after traveling a certain distance. This enables correcting chromatic aberration to a limited extent.
(N.B. In contrast, the angle at which a surface reflects photons is the same for all wavelengths and does not depend on its refractive index. That is why mirror telescopes are preferred over lens telescopes.)
p.28
If the denser medium has a sufficiently high refractive index compared to the less dense medium, photons arriving at sufficiently shallow angles of incidence get trapped.Instead of exiting the photons get diffracted so much they stay inside:

Internal Refraction is the basis of fiber optics. The ability to transmit light by flexible fibers makes medical and industrial endoscopes possible. Single fibers can be chronically implanted in neural tissue for optogenetic stimulation and recording. They can also be used as light pipes for daylight illumination of interior spaces.
Thanks to their disobeying the Pauli Exclusion Principle, photons of many different wavelengths can be travel through a single optic fiber simultaneously. This wavelength multiplexing combined with a lack of field interference when many fibers are packed together, enable optical fibers to carry more information than electrical wires.
p. 29
The above illustrations of refraction had the photons entering and leaving parallel surfaces. Consequently they continued in the same direction afterwards. However, if the two surfaces are not parallel, the photons will exit in a different direction. Here is an example:

When these photons exit a medium across a perpendicular surface, their diffracted direction is not changed. (All parts of the wave escape at the same time.)
Non-parallel media surfaces are the basis for changing the direction of light.
