11 WHERE PHOTONS CAME FROM

p. 30

A stack of appropriately shaped prisms can stop rays of photons from continuing to radiate:

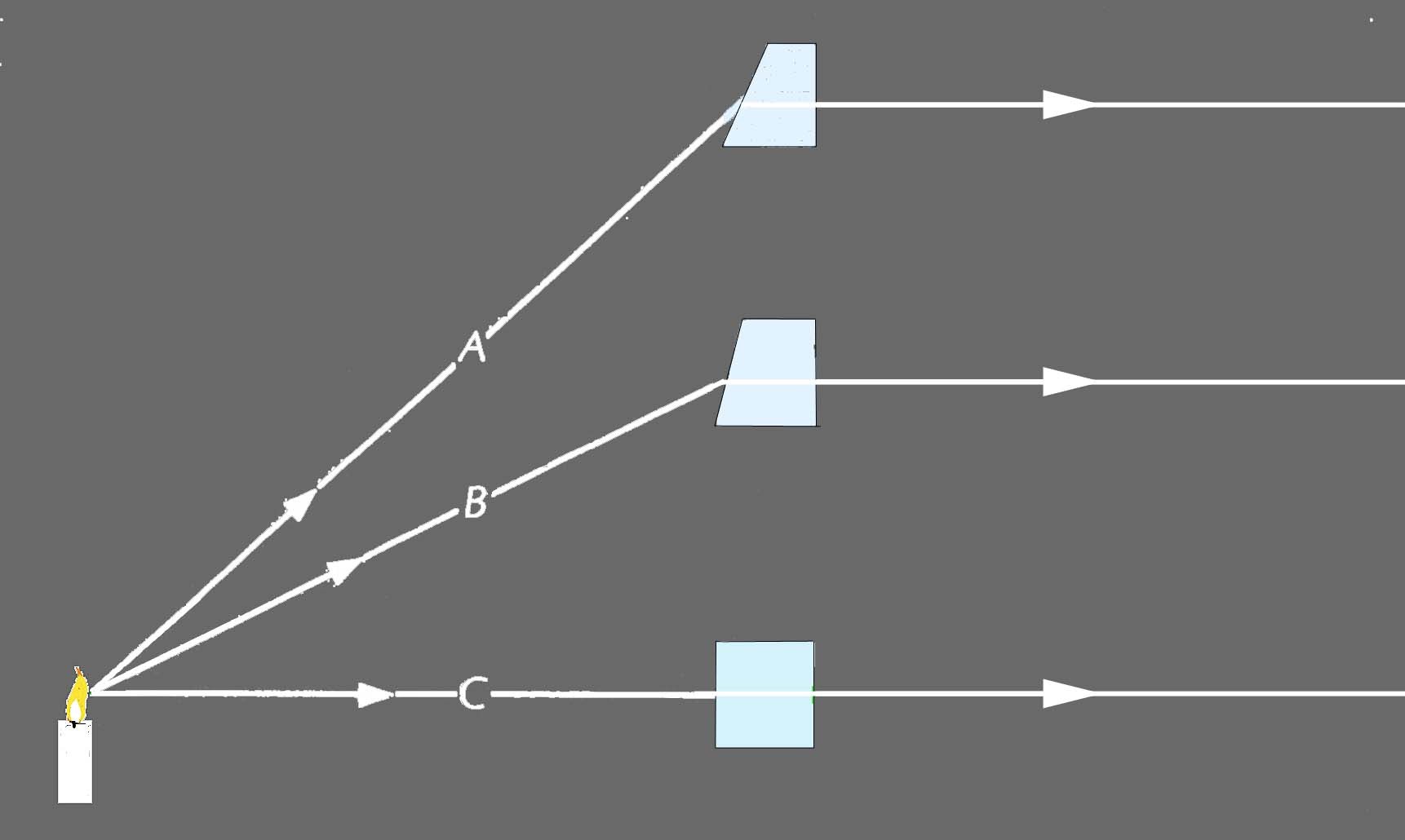
p. 31

One could add more prisms with “in-between” front angles to catch more rays radiating from the candle. However, there is a simpler solution. It turns out that a continuous curved surface can do the same thing.

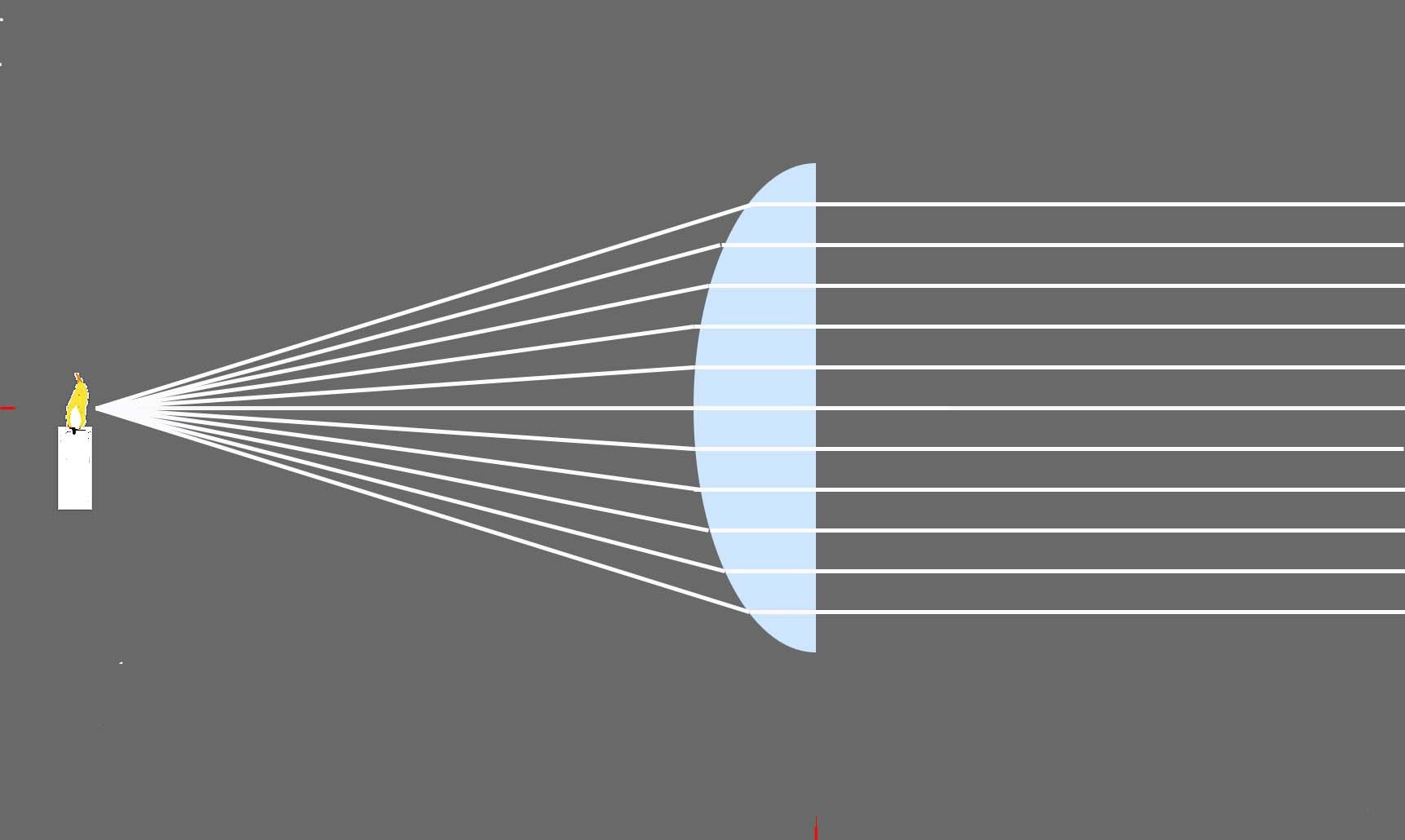
Lenses like this enable projecting rays of photons radiating from a source to a distant location without the loss of intensity with distance squared. The process of producing parallel rays of photons so they form a beam is called collimation.

p. 32

Any given lens curvature only bends the rays a certain amount depending on its refractive index. The above lens only collimated the rays from a candle at a certain distance.

Rays from a closer candle enter the lens at angles too steep be bent parallel. They still spread out, though less. Those rays from a further candle that reach the lens, diverge less. Being diffracted the same amount as rays from the other candles, they get bent too much and converge:

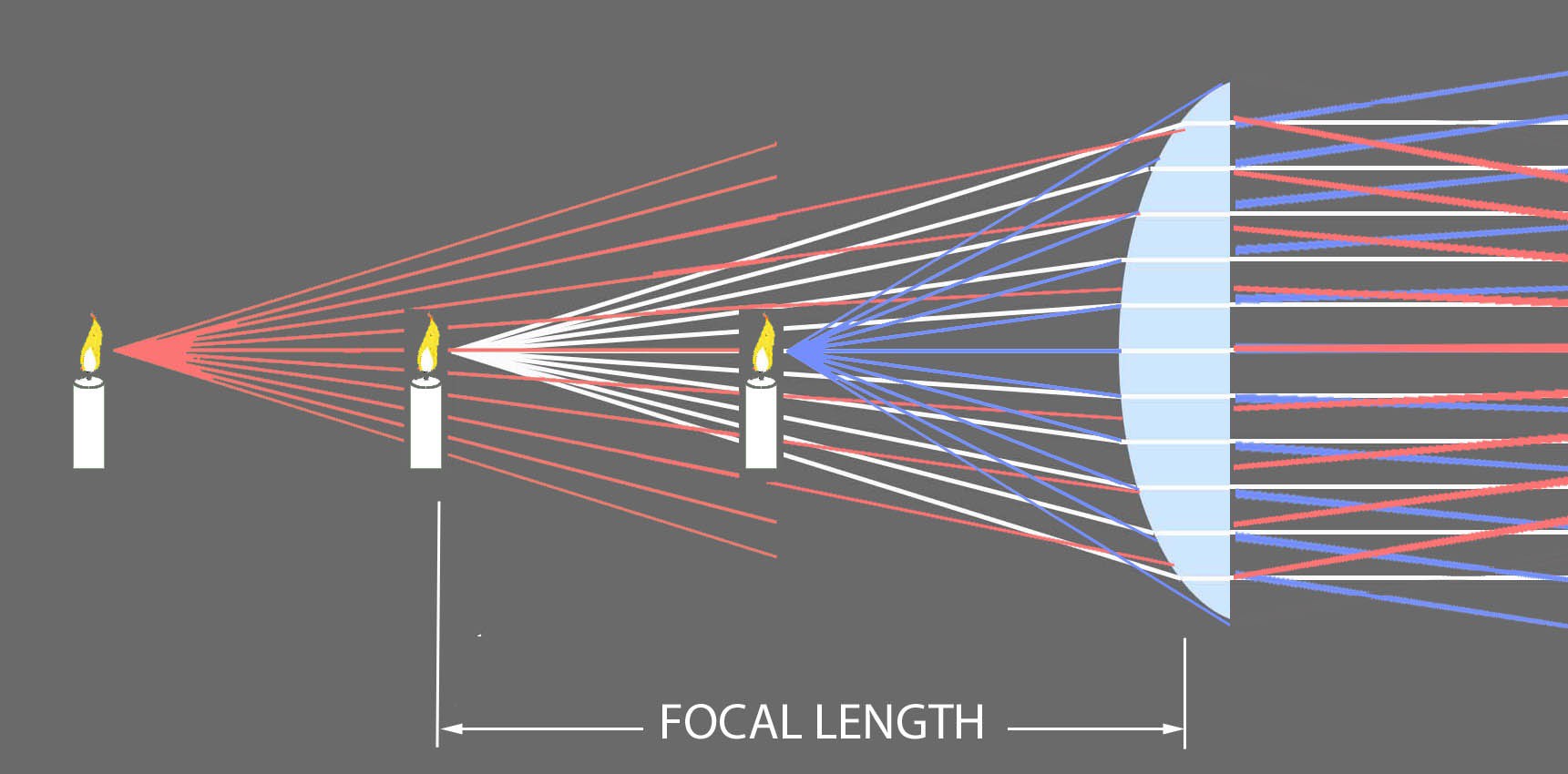
The source distance at which a lens produces collimated rays is the lens’ focal length.

p.33

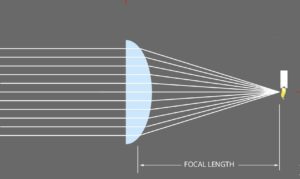
Now consider the reverse of the above figure. (Physicists are fond of proclaiming that their laws are the same regardless of the direction of time.) But rather than think backwards, let’s reverse the above figures. Now rays from a candle far out of sight to the left are collimated when they arrive.

A distance over 3 meters is far enough for most optical applications.

Therefore the rays from that candle will converge to a point a focal length behind the lens. At that distance there is an image of that candle:

But the image is upside down ?

Though off page, the real candle is right side up.

To see why the image is inverted, follow the rays on the next page:

p. 34

By bending the rays even more, it is possible to bring them all back together for an image of a source that is closer than infinity. This could be done with steeper rounding of the front surface of the above lens.  However, recall that light also gets bent when it speeds up as it leaves a denser medium. Also recall that Lambert’s Law operates in reverse too – rays striking a surface at a steeper angle enter less effectively.  Therefore a more elegant solution is to curve both sides of the above lens:

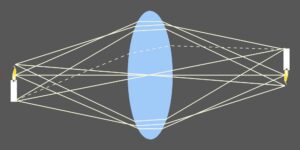
Simple geometry determines that lenses invert (and also reverse) the resulting image

p. 35

Two geometric principles govern how simple lenses transmit rays:

1. 1. Rays passing through the lens’ center continue in the same direction.

2a. Rays passing through the lens’ focal point emerge perpendicular to the lens.

or – since rays work the same in reverse

         2b. Rays perpendicular the lens pass through its focal point after emerging.

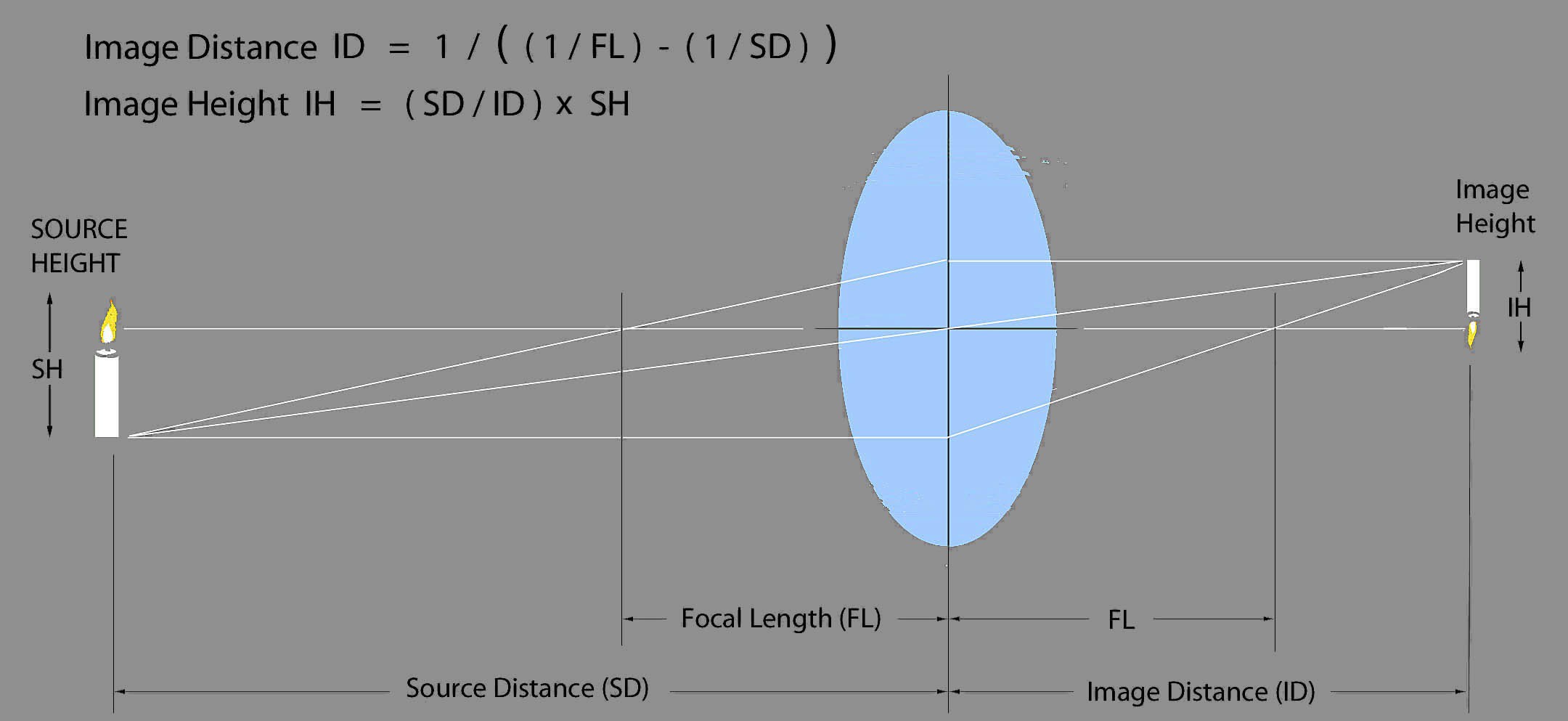
Distance and size of an image depend only on source distance and the lens’ focal length – ideally.

p. 36

Now For That Page 15 Question About Brightness And Distance:

Since light intensity decreases with the square of distance from a source, why don’t lamps get dimmer as you back away from them?

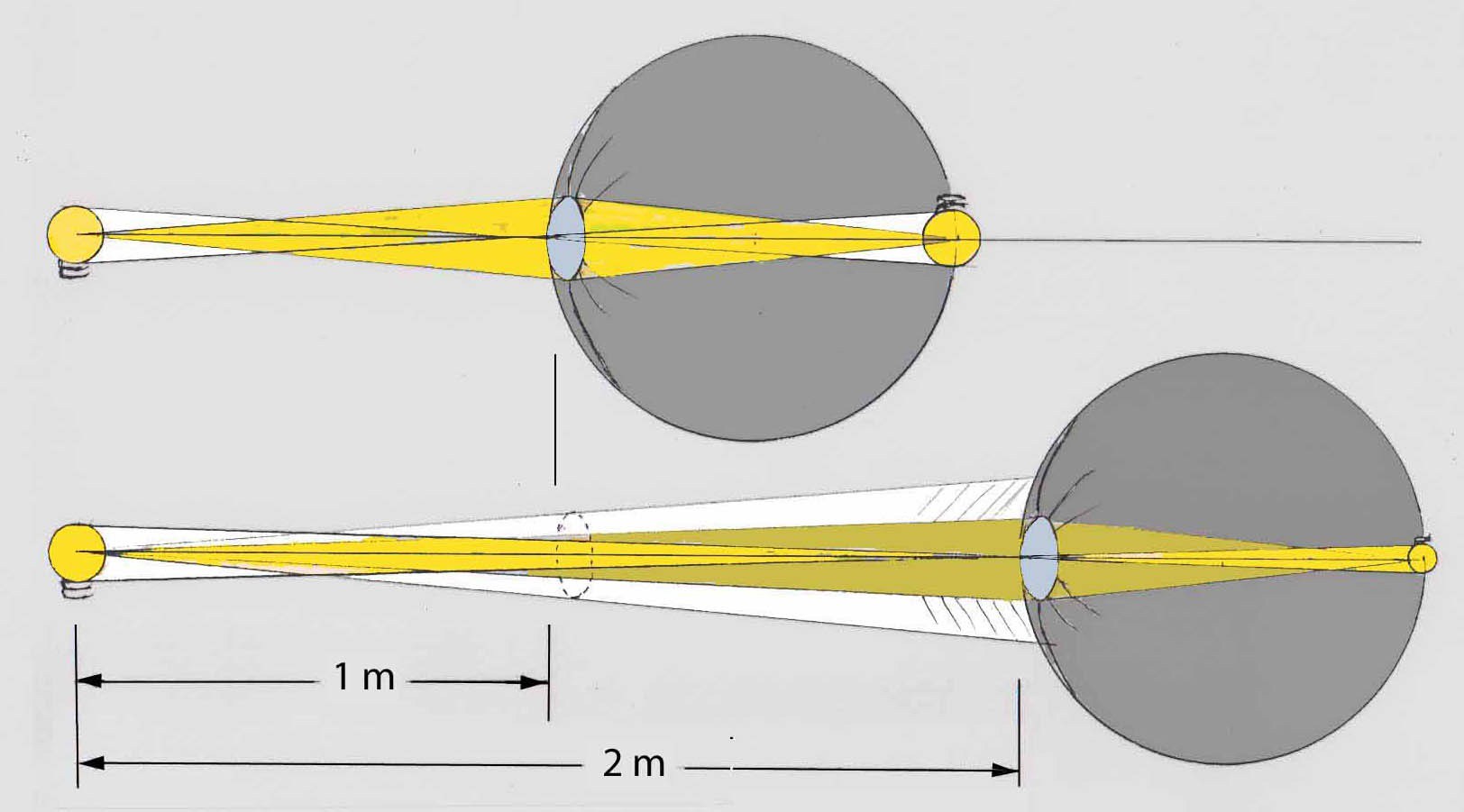
Only 1/4 as many photons reach the eye at 2 meters. However, the image extends over only 1/4 as much area. Therefore the image is just as bright.

The same occurs at any distance for any thing that emits or reflects photons.