Main Body
6 PHOTONS ARE REFLECTED
p. 16
There are relatively few natural sources of visible light in our world: sun, moon, stars, wild fires, volcanoes. We would live in darkness if most of the surfaces around us did not reflect photons from those sources.
Reflection can be characterized by how photons leave again after encountering either of two ideal surfaces:
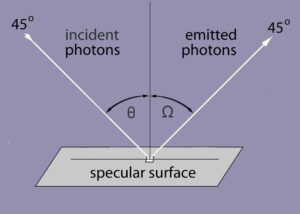
SPECULAR REFLECTION
Some surfaces are mirror-like and perfectly smooth. How photons “bounce”* off them is entirely predicable. The angle at which they leave equals the reverse of the angle at which they hit – Snell’s Law.
ANGLE OF INCIDENCE θ
=
Ω ANGLE OF EMISSION
LAMBERTIAN REFLECTION
These surfaces appear uniformly dull. At the microscopic level, they can be likened to being very bumpy. Therefore photons “bounce” off them in various directions even while each obeys Snell’s Law.
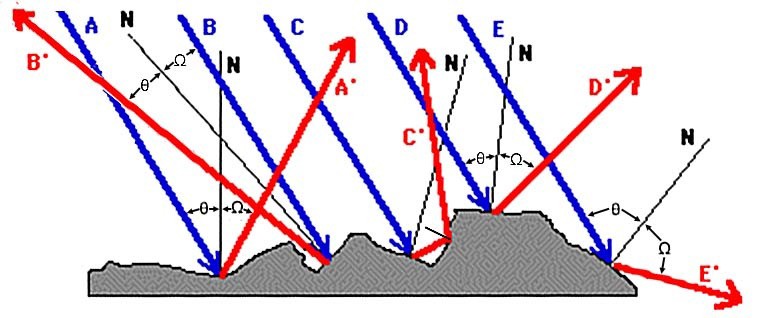ANGLE OF INCIDENCE θ
=
Ω ANGLE OF EMISSION
p. 18
An ideal such surface reflects photons similarly to how blackbodies radiate them – obeying Lambert’s Law.
The length of these reflected rays at various angles illustrates their intensity: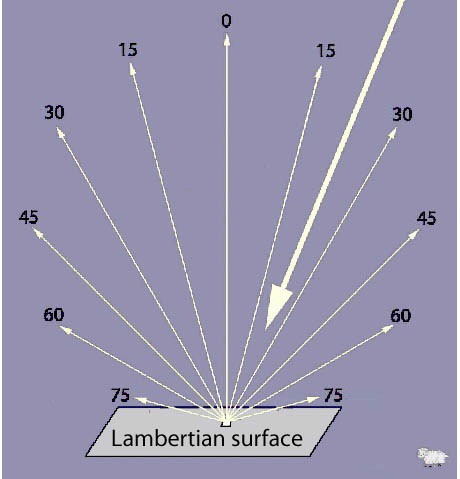 
Whether emitting or reflecting light, such ideal surfaces are said to be Lambertian.
p. 19
Despite the reduction in amount of light reflected at various angles, you may have noticed that dull surfaces still tend to appear equally bright regardless of the viewing angle!
At first counterintuitive, it is logical when one considers the size of the “per unit area” doing te reflection. Viewed head-on (at 0o ) that unit area appears largest. It decreases at larger angles to the same extent as the amount reflected decreases. Thereby the amount of light received per apparent unit area stays the same.
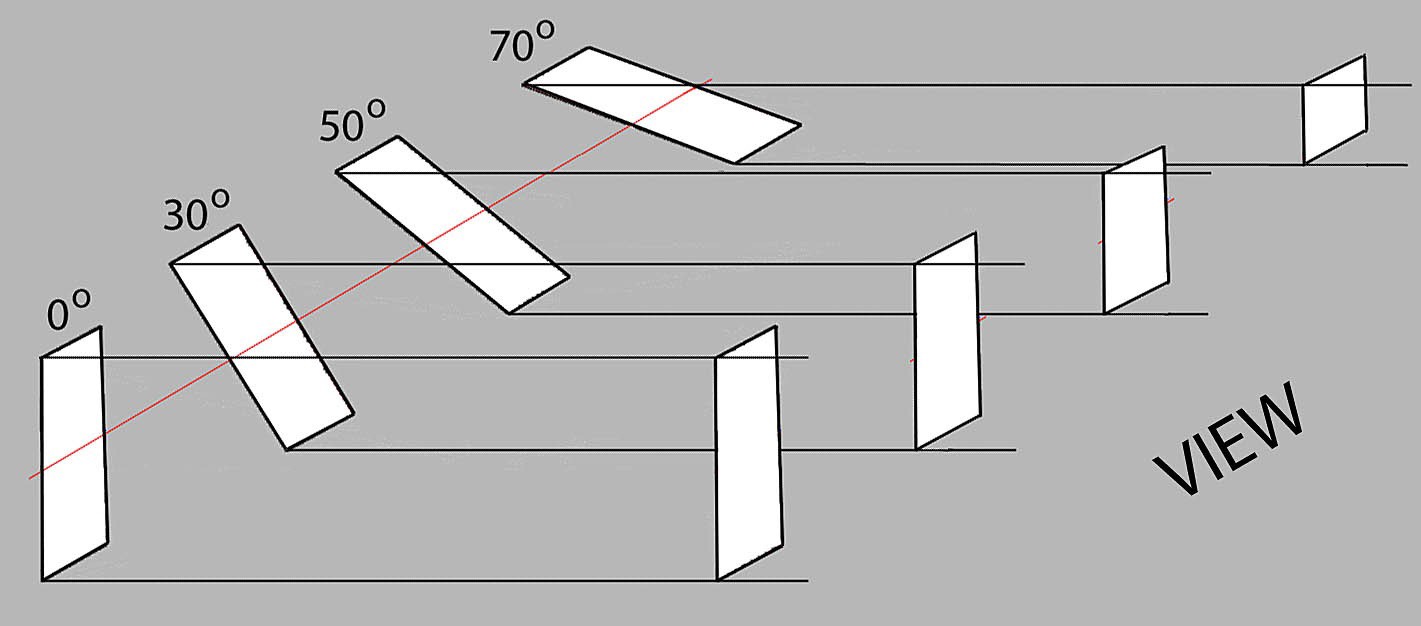
Few actual surfaces come close to either ideal. Most are blend of specular and Lambertian properties. However, this analytic approach helps approximating actual situations. This can be useful in for designing lighting environments.